Riassunto: Viene mostrata l’analisi spettrale di tre serie proxy tra quelle citate da Abbot e Marohasy(2017) in un lavoro di applicazione a reti neurali artificiali (ANN) per confrontare il contributo antropico rispetto a quello naturale nel cambiamento climatico.
Abstract: Spectral analysis of three proxy series quoted by Abbot and Marohasy (2017) is presented. These authors use artificial neural network (ANN) in order to compare antropogenic and natural contribution in climate change.
Introduzione
Abbot e Marohasy (2017, d’ora in poi AM17) usano una rete neurale artificiale per simulare le temperature del 20.mo secolo partendo dall’analisi (anche spettrale) delle temperature disponibili fino al 1830. Queste temperature sono in genere derivate anche da dati di prossimità (proxy), in particolare da anelli di accrescimento di alberi in varie regioni del globo. Vengono citati anche i dati derivati da una stalagmite in Cina e utilizzate le informazioni provenienti da ricerche archeologiche e racconti orali relativi al nord-ovest della Groenlandia.
Una volta che il modello (ANN) ha incamerato le informazioni, le usa per estrapolare le temperature del 20mo secolo. La differenza tra le temperature osservate e quelle calcolate è poi usata come indicazione del contributo umano al riscaldamento globale. Diciamo subito che gli autori trovano che il contributo naturale è preponderante rispetto a quello antropico.
Riassumendo: la rete neurale riceve in ingresso i parametri spettrali – periodo (o frequenza), ampiezza e fase ricavati dagli spettri delle serie proxy – e produce in uscita una serie di temperature dell’aria “previste” per il 20mo secolo, essenzialmente un modello delle temperature da confrontare con quanto si osserva.
Come è noto, il rapporto IPCC AR5 stabilisce che le temperature superficiali medie globali sono aumentate di 0.85 °C dal 1880 al 2012 e che il riscaldamento dal 1900 in poi è attribuibile all’aumento di concentrazione dei gas serra, dovuto alle attività umane. L’attribuzione è basata sui GCM (Global Climate Models) dai quali deriva una sensibilità climatica all’equilibrio (ECS) di 3.2°C.
In pratica, un raddoppio della concentrazione di gas serra (in particolare CO2) porterebbe ad un aumento della temperatura media globale di 3.2°C (la stima ha un orizzonte temporale, che è quello dei modelli, e si riferisce al 2100. Qui possiamo considerare sottinteso questo orizzonte).
Il concetto di ECS nasce storicamente da un lavoro di Arrhenius del 1896 che prevedeva un aumento di 5-6°C. La sua stima è andata progressivamente diminuendo ma quella derivata dai modelli globali è nettamente più alta di quella che proviene da metodi di spettroscopia sperimentale, i cui valori sono attorno a 0.5-0.6°C (e, in alcuni casi, anche inferiori). È chiaro dalla definizione di ECS che, se le stime fossero quelle spettroscopiche, l’AGW, ancor più l’AGW catastrofico o CAGW, non esisterebbe al tavolo della discussione politica, con profonde conseguenze sociali, nel bene e nel male.
In AM17 i modelli di temperatura dell’aria (regionali e globali), generati da reti neurali, portano a valori stimati di ECS pari a 0.6-0.8°C. Il risultato è simile a quello da spettroscopia e da modelli di bilancio energetico (0.4-2°C) ma è lontano dalla stima da GCM e da studi paleoclimatici (2-3°C).
Confronti
L’uso dell’analisi spettrale per generare onde sinusoidali che siano l’input per una rete neurale implica sia l’uso di serie proxy che la selezione di periodicità disponibili in letteratura: AM17 elenca una notevole bibliografia di risultati spettrali e di periodi caratteristici che si riferiscono a fenomeni naturali (sole, oscillazioni oceaniche, El Nino, ecc, e relazioni tra loro).
Mi sono posto il problema di verificare almeno in parte i periodi spettrali citati in letteratura, ma mi sono scontrato con l’impossibilità o la difficoltà di disporre delle serie usate dai vari autori.
Wilson et al., 2007
In particolare ho apprezzato il lavoro di Wilson et al., 2007, un’attenta e dettagliata analisi spettrale di temperatura derivata da anelli di accrescimento di 22 siti (+9 analizzati ma poi non usati) del Golfo dell’Alaska (GOA). Nell’articolo, però non sono forniti i dati da cui si parte (temperatura superficiale dell’aria, del periodo gennaio-settembre), anche se sono una complessa combinazione, seguita da calibrazione e detrending, di quanto si osserva nei 22 siti selezionati. Wilson si limita a mostrare grafici difficilmente gestibili e a fornire periodi spettrali ottenuti con MTM (Multi Taper Method): 10-11, 13-14, e 18-19 anni e con SSA (Singular Spectrum Analysis): 14.1, 15.3, 24.4, 38, 50.4, 91.8 anni. Non è quindi possibile verificare se la serie, estesa dal 700 al 1999, mostri periodicità più lunghe (o più brevi) di quelle elencate.
| Rob Wilson appare come uno scienziato molto serio e consapevole delle “bufale” che possono derivare dai proxy. In particolare è molto critico nei confronti dell’Hockey Stick di Mann. Nel sito Bishop Hill ho trovato questa testimonianza di Andrew Montford -il proprietario del sito- che ha assistito ad una lezione di 2 ore di Wilson nel 2013. |
Mentre scrivevo queste righe ho pensato che, invece di lamentare la mancanza di dati, avrei potuto scrivere a Wilson per chiederli a lui direttamente. L’ho fatto e nel giro di tre ore ho ricevuto il link ai dati del 2007 e quello ad una elaborazione successiva che qui non uso. Nella sua risposta Rob Wilson mi fa notare che, a causa del detrending, sarebbe stato difficile trovare periodi più lunghi di 100 anni (NB. The detrending of the data will make it difficult to find a strong centennial signal I think.).
Invece in fig. 1 (pdf) si osservano tre massimi spettrali oltre i 100 anni (e non identificati in Wilson et al., 2007) di cui uno, a 222 anni, è il massimo assoluto dello spettro.

Date le ampie incertezze nelle misure degli anelli e nelle cause che possono averli fatti crescere o meno, credo che il massimo principale possa essere associato al ciclo solare di de Vries (o Suess) di 208 anni. Nello spettro si vedono i massimi a 14.1,15.4, 18.1, 23.8, 38 e 92.8 anni, coincidenti o largamente compatibili con quelli già elencati sopra; si vedono anche i tre intervalli calcolati da Wilson con MTM.
L’analisi conferma i risultati di Wilson et al., 2007 e aggiunge un forte segnale, probabilmente solare, e una “firma” di El Niño, non particolarmente potente ma ben visibile.
Infine, e solo a titolo di curiosità, noto la presenza del massimo a 2.87 anni, una mia vecchia “fissazione”, istigata da un commento di Donato Barone, v. ad esempio qui, su CM.
Tan e Liu, 2003
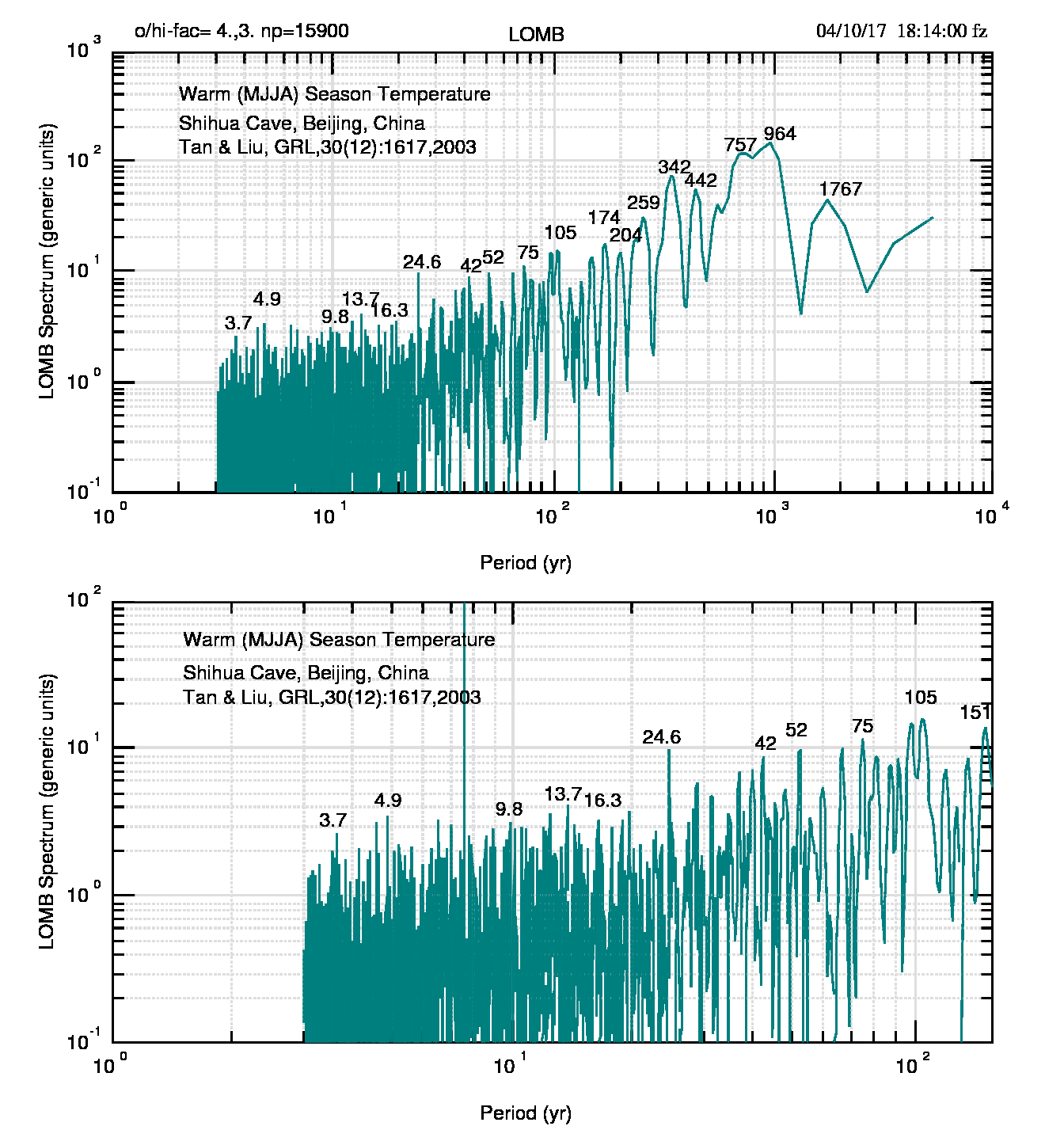
Un’altra serie disponibile, tra quelle elencate da AM17, è Tan e Liu, 2003. La temperatura è derivata da una stalagmite nella cava di Shihua, Pechino e la serie copre un periodo di 2650 anni, dal -650 al 2000. Il suo grafico è mostrato in fig.2 (pdf).

Per AM17, da questa serie si deducono periodi significativi a 206 e 325 anni, mentre gli autori aggiungono anche 750 e 900 anni
Lo spettro Lomb, mostrato in fig. 3 (pdf), con alcune differenze poco significative, conferma le quattro periodicità ma racconta una storia molto più articolata e complessa: ad esempio sono visibili tutti i periodi identificati nello spettro GOA di Wilson ma anche i periodi (3-6 anni) legati a El Niño, quello a 9.8 anni legato all’interazione sole-pianeti e quello a 342 anni, tutti presenti nello spettro di Wilson.
Moffa-Sanchez et al., 2014
usa carote di sedimenti marini per analizzare la variabilità idrografica della Corrente Nord-Atlantica (NAC) negli ultimi 1000 anni. La NAC è importante per il trasporto di sale verso le alte latitudini e il sale è un prerequisito per la formazione di acque profonde, a loro volta essenziali per AMOC (Atlantic Meridional Overturning Circulation) e quindi per il sistema climato generale. In più il calore prodotto da NAC -e trasportato dai venti occidentali- contribuisce ad un clima migliore in Europa.
Gli autori di questo lavoro sono interessati al confronto tra temperatura, salinità, rapporto Mg/Ca e alla loro relazione con l’irraggiamento solare (TSI, Steinhilber et al, 2009).
Avevo ricevuto i dati relativi a questo lavoro nel marzo 2014 da Paola Moffa-Sanchez e li avevo elaborati allora, ma mai pubblicati.
Mostro qui in fig. 4 (pdf) il confronto tra le variabili e la relazione con TSI.

Dall’analisi spettrale wavelet gli autori derivano periodi significativi compresi tra 135 e 225 anni, ma trovano anche 30, 16,14 anni.
Lo spettro che ho calcolato io, fig. 5 (pdf) non conferma, o conferma molto vagamente, l’analisi spettrale del lavoro. In particolare, dei tre periodi più brevi trovo solo quello di 14 anni e l’intervallo 135-225 anni, oltre ad essere poco preciso, non include il secondo massimo più potente che trovo a 261.5 anni (però ricorda molto due dei tre massimi di periodo più lungo nello spettro di Wilson, in fig.1). Il mio massimo più potente, a 50.3 anni, presente anche negli spettri di Wilson e di Tan e Liu, non viene citato. Da notare che, malgrado la fig.4d faccia pensare diversamente, l’analisi spettrale mostra una relazione quasi inesistente con l’irraggiamento solare.

Conclusioni
Le conclusioni che si possono derivare sono simili a quelle del post scritto insieme a Luigi Mariani: le tecniche di intelligenza artificiale fanno sperare in un futuro davvero interessante, ma per ora usano solo una minima parte delle complesse interazioni tra le variabili climatiche evidenziate dall’analisi spettrale.
| Tutti i grafici e i dati, iniziali e derivati, relativi a questo post si trovano nel sito di supporto qui. |
Bibliografia
- John Abbot and Jennifer Marohasy: The application of machine learning for evaluating anthropogenic versus natural climate change, GeoResJ, 14, 36-46, December 2017.doi:10.1016/j.grj.2017.08.001.
- Arrhenius S : On the influence of carbonic acid in the air upon the tempera- ture of the ground. Philos Mag, 41(5), 237-76, 1896 .
- Ming Tan and Tungsheng Liu: Cyclic rapid warming on centennial-scale revealed by a 2650-year stalagmite record of warm season temperature , GRL, 30, 191-194, 2003. doi:10.1029/2003GL017352
- Paola Moffa-Sánchez, Andreas Born, Ian R. Hall, David J. R. Thornalley and Stephen Barker: Solar forcing of North Atlantic surface temperature and salinity over the past millennium,Nature Geoscience , 7, 275-278, 2014. doi:10.1038/NGEO2094
- Steinhilber, F., J. Beer, and C. Fröhlich. Total solar irradiance during the Holocene. Geophys. Res. Lett., 36, L19704, 2009. doi:10.1029/2009GL040142
- Rob Wilson, Greg Wiles, Rosanne D’Arrigo and Chris Zweck: Cycles and shifts: 1,300 years of multi-decadal temperature variability in the Gulf of Alaska , Clim Dyn, 28, 425-440, 2007.doi:10.1007/s00382-006-0194-9.


Ciao a tutti,
sebbene in ritardo, vorrei fare qualche commento strettamente tecnico e strettamente on-topic.
Premessa: nel mio essere un non professionista ritengo che per l’analisi delle quasiperiodicita` naturali le CWT (Continuous Wavelet Transform) siano l’approccio migliore, visto che oltre a mostrare gli spettri di potenza ne mostrano il cambiamento.
(magari qualcuno si ricordera` il mio lavoro del 2005 sul proto-CM [quando ancora era un forum] sulle analisi CWT/XWT su macchie solari, T globali e indici climatici…)
Nel paper viene usata una rete “general regression” (GRNN), che /nomen omen/ e` l’architettura piu` generale per il calcolo delle regressioni. Tralasciando il fatto che venga usato un software proprietario/commerciale e che non vengano specificati i parametri (Hyperparameters, in gergo) della rete ne` il numero di cicli di training (epoche), informazioni che nel machine learning sono abbastanza rilevanti, c’e` una cosa che mi preme specificare: in quell’architettura di rete fondamentalmente manca la gestione della dimensione *tempo*.
Le reti neurali ricorsive (RNN), ed in particolare le reti LSTM (Long Short Term Memory) sono decisamente piu` adatte all’analisi delle variazioni temporali, in quanto ogni strato non solo analizza l’input corrente ma anche quelli precedenti (al contrario delle GRNN che sono ad una sola passata). Strato dopo strato, passata dopo passata, correlazioni sempre piu` generali emergono su tutta la sequenza di input.
Un approccio in tal senso e` stato usato qui: https://arxiv.org/pdf/1705.06861.pdf per fare forecast sulle SST con ottimi risultati: basti guardare la figura 5 alla fine del paper per vedere la differenza tra una rete LSTM e una rete RBF (le GRNN sono piu` o meno delle generalizzazioni delle RBF).
Posto che io non credo nella scienza che non sia *completamente open source*, ritengo che il problema della scienza “settled” (soprattutto, ma non solo) non sia solo culturale, ma anche metodologico: al di la` dei climateleaks del 2009 (qualcuno si ricordera` questo http://www.climatemonitor.it/?p=5551 etc etc) di *codice sorgente* se ne e` visto poco, impedendo /de facto/ una *vera* peer review, dove peer equivale a *tutti* e implica la _riproducibilita`_ da parte di tutti e celando un tipo o l’altro di bias dietro l’information hiding. Quindi, in questa mia visione, e` IMHO “settled” anche AM17.
Da qui la mia idea che mi tormenta da quando ho letto questo post su CM. Uso il termine /tormentare/ perche` potrebbe anche essere ora, per me, di uscire dal guscio.
Prendere due reti LSTM, ad una si danno in pasto i dati grezzi delle serie e all’altra gli spettri delle CWT. Fargli generare i dati successivi e *gli spettri successivi* da cui fare prediction, farle co-convergere. Qualche centinaio di righe di codice di Python, Keras, Tensorflow e SciPy. Tutto completamente open-source su github. Chi ha voglia di salire di un gradino?
Daniele vorrei sapere che aspetti.
gg
…e nemmeno io Franco, ma è un piacere parlarne con te 🙂 grazie!
@ Massimo Lupicino (il sistema non mi permette il reply)
Massimo, non vedo particolari difficoltà nel massimo tra 2 e 3 (~240 mila anni): si colloca nello schema di un massimo ogni 100 mila anni, periodicità che quasi tutti attribuiscono al ciclo di Milankovich (eccentricità orbitale). Io ho smesso di credere all’influenza dell’eccentricità dopo il post che ho citato nell’altra risposta, ma questo non toglie che la periodicità a 100 mila anni ci sia e che il massimo a 240 mila anni sia, come dire, “al suo posto”.
Il viaggio verso l’interglaciale è sempre più veloce di quello verso il glaciale: è come se si innescasse un processo che accelera il riscaldamento.
In tutto questo “gioco”, non ho ben capito il ruolo e l’influenza del ghiaccio terrestre: assorbe e rilascia CO2 anche lui, ma con quali ritmi rispetto al ghiaccio oceanico? Quanto pesa nella salita rapida e nella discesa lenta? Franco
Caro Franco posso solo dirti che la tua idea mi convince e mi piace. Ammesso che la fugacita’ della co2 in fase solida e a temperatura molto bassa sia notevolmente inferiore a quella in fase liquida e a temperatura molto più alta (assunzione legittima direi :)) si può concludere che durante il riscaldamento lo scioglimento dei ghiacci si associa ad un feedback positivo (più se ne scioglie più co2 si libera), mentre nel caso opposto il feedback è negativo (piu acqua si solidifica e meno co2 viene riassorbita dall’acqua (meno superficie liquida disponibile) e tanto meno dal ghiaccio.
Che ne pensi?
Caro Massimo, sono completamente d’accordo: il meccanismo che proponi è molto sensato e “mi suona” bene. Gran parte dei cambiamenti (glaciazione e scioglimento) dovrebbe avvenire come scrivi. Per i dettagli, nei quali come si sa si nasconde il diavolo, non credo di avere le competenze necessarie.
Franco
Caro Franco, complimenti per il bel lavoro che hai portato a termine e grazie per averci messo al corrente di questo importante contributo alla comprensione delle dinamiche del clima.
Personalmente sono sempre piuttosto perplesso riguardo alle estrapolazioni: prevedere è il compito della scienza, ma in campo climatologico le previsioni lasciano il tempo che trovano.
La non linearità del sistema climatico è tale, infatti, da rendere sempre molto problematiche le previsioni. Nella fattispecie gli autori estrapolano a dopo il 1830 le serie di dati di prossimità raccolte fino ad oggi e le confrontano con le temperature rilevate. Mi rendo conto di aver semplificato molto perché ciò che viene estrapolato sono le periodicità, ovvero le regolarità evidenziate nei secoli precedenti, ma il principio rimane lo stesso: si presume che il comportamento del clima nei secoli sia regolare e io ho qualche dubbio in proposito.
Fatta questa premessa, ho trovato molto interessante il discorso relativo alla sensibilità climatica all’equilibrio che scaturisce dall’articolo: essa dovrebbe essere molto più bassa di quanto hanno trovato anche i ricercatori più ottimisti in materia di squilibrio radiativo e che vengono tacciati di negazionismo. Considerato che la sensibilità climatica all’equilibrio è calcolata sulla base di dati di prossimità e che anche il risultato di Abbot et al., 2017 si basa su dati di prossimità, ho l’impressione che il confronto con gli altri valori della letteratura sia omogeneo.
Le verifiche da te effettuate con MEM e Lomb che danno dei risultati in linea con quelli di Abbot et al., 2017, mi fanno sperare che il dato dell’ECS sia abbastanza robusto. Bisogna augurarsi che di esso tengano conto i revisori dell’IPCC in occasione del prossimo report.
Ciao, Donato.
p.s.: noto con piacere che il periodo di 2,87 anni fa capolino spesso nelle analisi delle serie climatologiche. 🙂
Caro Donato,
credo che le reti neurali facciano più che semplicemente estrapolare, sulla base di un’equazione, dati del passato verso il futuro. Esiste un processo di apprendimento che permette a questi sistemi di “scegliere”, seguendo quanto hanno acquisito. Pur non sapendone molto, mi permetto il lusso di
avere speranze sui loro sviluppi futuri ma, per ora, noto e quando posso registro il fatto che le scelte sono limitate solo ad alcune frequenze (con relative ampiezza e fase), trascurandone altre che appaiono spesso negli spettri di dataset molto diversi gli uni dagli altri.
Secondo me è una mancanza importante, credo derivata dalla scelta di privilegiare i livelli di confidenza, rispetto ai quali si definisce la natura di fluttuazione di massimi spettrali che in realtà sono reali perché sono confermati da altri dataset, anche indipendenti.
Mi sono fatto l’idea che la climatologia dovrebbe prendere atto del fatto che la frequenza di occorrenza (quasi indipendentemente dalla potenza) è più importante del superamento o meno del livello di confidenza.
Ho scritto queste cose anche a Rob Wilson, che si occupa anche di spettri oltre che di anelli di accrescimento, e spero di avergli messo una (piccola) pulce nell’orecchio. Chissà, magari la pulce crescerà … aiutata dagli spettri che ho calcolato per tutti i suoi dataset e che gli ho mandato.
Sì, il “nostro” periodo di 2.87 anni capita spesso: spero, prima o poi, di capire a cosa potrebbe essere attribuito. Ciao. Franco
Nel ringraziare per questo interessante contributo, mi permetto di chiedervi di aiutarmi a capire se e come il coefficiente alpha (in Wm-2, ) della formula di Arrhenius, Δ F = α ln ( C / C 0 ), sia comparabile ai valori di ECS (in °C) ottenuti con la formula
ECS=F2×CO2 * ΔT/(ΔF−ΔQ)
In questa equazione è introdotto il forcing radiativo attribuibile al raddoppio della concentrazione atmosferica di CO2, F2×CO2, che secondo l’IPCC (AR5) ha un valore centrale di 3.71 Wm−2, e che sarebbe quindi il parametro da confrontare con il valore di 5-6 Wm-2 del coefficiente di Arrhenius. La formula di Arrhenius tuttavia non utilizza il criterio del raddoppio di CO2 ma un incremento qualunque rispetto a una baseline.
E’ la mia mancanza di nozioni nella materia che rende difficile la mia comprensione di come questi concetti siano evoluti dai tempi di Arrhenius fino a oggi. Ringrazio quindi anticipatamente chi vorrà darmi un chiarimento.
Purtroppo non sarò io a chiarire l’argomento. Come ho già scritto in commento ad un post di Donato Barone di qualche tempo fa, per me ECS è poco più di un coefficiente moltiplicativo per far sì che le osservazioni tornino con i modelli, ma sicuramente mi sbaglio: troppe persone considerano questo un parametro importante perché possa essere io ad avere ragione. Però il fatto che continui ad abbassarsi mi fa ben sperare per il futuro.
Per la relazione tra ECS e i valori di Arrhenius, ho ripreso il testo dell’articolo di Abbot e Marohasy che scrivono:
“The external radiative forcing functions were initially based on the work of Svante Arrhenius in the 19th century, who first proposed that a doubling of atmospheric carbon dioxide could lead to a 5 to 6 °C increase in global temperatures”.
Non saprei cosa dire di più; speriamo che qualcuno voglia aiutarci. Franco
In effetti Arrhenius aveva previsto un aumento termico di 4.95-6.05 °C raddoppiando la concentrazione atmospferica di CO2. Con il coefficiente alfa=5.35 Wm-2 si arriva al valore di forcing radiativo (DF=3.71 Wm-2) accettato dall’IPCC.
Elementi di incertezza si ritrovano nel convertire il forcing radiativo in aumento termico. Le stime di Arrhenius sono eccessive perché implicano >1 °C per Wm-2. Per le stime attuali, un valore di riferimento è quello derivato da Rahmstorf, 2008, in: Zedillo, ‘Global Warming: Looking Beyond Kyoto’, pari a 0.8 °C per Wm-2. Ma altri autori hanno fornito valori più bassi: 0.173 (Idso, 1998, Climate Research), 0.35-0.54 (Shaviv, 2005, Journal of Geophysical Research).
Con questi elementi di incertezza, i valori stimati di ECS risultano quindi molto variabili: da 0.33 °C (Lightfoot et Mamer, 2014, Energy & Environment) ai 4.5 °C del limite superiore dell’IPCC.
Quindi la storia non finisce qui.
Una conferma di tutte le incertezze viene dalla figura 7 del secondo lavoro di Scafetta e C. citato oggi da Guido in http://www.climatemonitor.it/?p=46075
anche se da tutte le incerteze emerge la tendenza abbastanza netta di ECS a diminuire.
Prima o poi questa tendenza si fermerà e spero di vedere la fermata prima di … togliermi dai piedi -:). Ma credo anche io che la storia non finisca qui. Franco
Scusate la mia ignoranza in materia, qualcuno ha mai pensato che possa essere l’aumento della temperatura a far aumentare la quantità di CO2 e non il contrario?
Senza voler essere troppo categorico, direi che tutti gli scettici lo pensano (e forse anche qualche “credente”). I profili di temperatura e di CO2 delle carote antartiche e artiche mostrano che la CO2 segue la temperatura con un ritardo di circa 800 anni come si vede nell’immagine. Franco
Immagine allegata
Grazie per il bel grafico Franco. Ricordo un articolo sullo stesso argomento su CM diversi anni fa. Del resto che la fugacita’ della CO2 in acqua sia direttamente proporzionale alla temperatura della stessa acqua attraverso la tensione di vapore (legge di Raoult), e’ cosa nota da circa 130 anni. In altri termini, se il pianeta si scalda, qualche che sia la ragione, gli oceani DEVONO cedere CO2 all’atmosfera. E’ quello che ci si aspetta al termine di una glaciazione, per esempio.
Mi chiedo se qualcuno ha fatto l’esercizio di mettere quel grafico in relazione con la fine dei periodi glaciali, in cui aumento di temperatura e conseguente aumento di CO2 dovrebbero trovare riscontro. Direi che gli ultimi due periodi glaciali (Wurm e Riss) trovano pieno riscontro in questo grafico. Mentre questa correlazione non si vede granche’ per il Mindel…
Massimo, temo di non aver capito bene: il grafico (Vostok Ice Core) mette già in relazione temperatura e CO2 con i periodi glaciali (e gli interglaciali).
Comunque sì,dal grafico si vede bene che il periodo glaciale contrassegnato dal numero 4 (non sono tanto bravo con i nomi) presenta un visibile anticipo della CO2 rispetto alla temperatura.
Il motivo di questa inversione di tendenza non lo conosco ma potrei immaginare un cambiamento importante e, almeno per me, inspiegabile.
In questo sono confortato dalla fig 3 di http://www.climatemonitor.it/?p=44127
(trascuriamo la parte rossa del grafico) in cui un pianeta che andava tranquillamente verso la morte glaciale, con il d18O in costante aumento, ha incominciato (tra 0.5 e 0.7 Ma) a cambiare tendenza. Il quarto periodo glaciale è a ridosso (geologicamente) di questo cambiamento e avrebbe potuto
risentirne. Franco
Ciao Franco, grazie della risposta. Il problema e’ che non trovo coerenza tra l’andamento termico e alcuni interglaciali. Ad esempio il Mindel sarebbe collocato tra 300,000 e 450,000 anni, mentre tra 200,000 e 300,000 saremmo in presenza di un interglaciale, in mezzo al quale si colloca pero’ il picco tra il 2 e il 3. Sono domande tediose lo so, dovrei andare a studiarmi la cronologia delle glaciazioni e basta 🙂
Quello che conta e’ la relazione tra Co2 e variazioni di temperatura, che dal grafico si vede chiaramente. Insieme al fatto (correggimi se sbaglio) che sembra esserci un lag maggiore T-CO2 nelle fasi di raffreddamento rispetto a quelle di riscaldamento, come se la cinetica di assorbimento della CO2 da parte degli oceani fosse piu’ lenta rispetto a quella di rilascio della CO2 in atmosfera da parte degli oceani stessi…
Lo so che non è scientifico ma guardando il grafico delle anomalie termiche mi sono divertito a sovrapporci alcuni eventi storici
IV, V sec a.C. età Classica +1° di anomalia.
476 d.C. Caduta dell’ impero romano anomalia di -1°
Rinascita del 1000 da risalita da -1,8° a +1°
1300-1470 Rinascimento +1°
guerra dei trent’anni 1618 – 1648. -1,5°
Prima Rivoluzione industriale uso del carbone minerale al posto del carbone vegetale in esaurimento Seconda metà del 700 anomalia di – 0,7°preceduta da un secolo a -1,7°
Sembra che quando sia caldo si stia meglio e quando sia freddo stia decisamente peggio. ma come dicevo è una mia opinione non provata da un modello matematico
Non sono sicuro che sovrapporre eventi storici ad anomalie non sia scientifico: in ogni caso è un esercizio molto istruttivo per capire quando gli umani stanno meglio e si possono permettere qualcosa in più della mera ricerca di cibo.
Riporto sotto, un grafico che molti hanno sicuramente già visto, sempre utile, però, a ricordare che “al caldo si fa meglio”. Franco
Immagine allegata
Bellissimo questo grafico, molto didattico! Salvato per futura diffusione. Sto leggendo con attenzione l’articolo, che riesco persino a capire nelle sue linee generali :). Grazie davvero.
Prego.
Ho aggiunto al sito di supporto l’immagine a risoluzione maggiore (2MB) sperando di fare cosa gradita. Franco