I modelli di regressione: non è tutto oro quello che luce

Il prof. N. Scafetta, in questi ultimi tempi, si sta interessando al problema del livello del mare e della sua evoluzione futura. Dopo il recente articolo…

Multi-scale dynamical analysis (MSDA) of sea level records versus PDO, AMO, and NAO indexes – (pdf)

…di cui ho avuto occasione di parlare qui, è stato da poco pubblicato un nuovo lavoro che, però, si occupa di un problema ancora più generale: gli errori nell’applicazione dei modelli di regressione e dei filtri wavelet utilizzati per analizzare i segnali geofisici.

Discussion on common errors in analyzing sea level accelerations, solar trends and global warming

  – (pdf)

Nell’articolo, piuttosto corposo e denso di spunti di riflessione molto interessanti, il prof. N. Scafetta accentra la sua attenzione su tre aspetti che rivestono molta importanza nel dibattito in corso tra i membri della comunità scientifica che si occupano di climatologia, in generale, e dei suoi aspetti più particolari (temperature, livello dei mari, contenuto di calore degli oceani, paleoclima ecc., ecc.) Secondo quanto scrive il prof. N. Scafetta nel suo articolo (da ora Scafetta, 2013b) buona parte degli studi che sono stati effettuati fino ad oggi sono affetti da errori ed approssimazioni eccessivi in quanto non tengono conto di tre importanti fonti di errore.

1. Per quantificare correttamente l’accelerazione della variazione del livello del mare è necessario tener conto delle oscillazioni naturali multidecadali quantificate dagli indici AMO (Oscillazione Atlantica Multidecadale), NAO (Oscillazione Nord Atlantica) e PDO (Oscillazione Pacifica Decadale).
2. Le forzanti del clima non sono conosciute in modo approfondito e le incertezze nella loro quantificazione impediscono di leggere con chiarezza il contributo del forcing solare all’aumento delle temperature superficiali del pianeta nel corso del 20° secolo. Gli effetti di tali incertezze, inoltre, sono amplificati dalla circostanza che molte di queste forzanti non sono indipendenti tra di loro per cui i modelli matematici risentono fortemente della dipendenza lineare delle funzioni matematiche che le schematizzano.
3. I filtri wavelet periodici nati per filtrare segnali di tipo stazionario, vengono comunemente applicati a segnali, come quelli geofisici, caratterizzati da una spiccata non stazionarietà. Questo determina numerosi artefatti analitici che alterano profondamente la natura dei dati soggetti al trattamento di filtraggio.

Rimuovendo queste tre cause di errore, Scafetta, 2013b è giunto a delle conclusioni estremamente interessanti.

L’aumento della velocità di variazione del livello del mare misurato dal mareografo di New York, sulla base dello studio condotto da Sallenger et al. 2012, risultava essere estremamente forte, tanto da far temere che le previsioni secolari IPCC AR4 circa l’aumento del livello del mare, potessero sottostimare il valore del livello del mare al 2100. Tale conclusione viene confutata dallo studio di N. Scafetta, 2013b in quanto l’incremento del livello del mare al 2100, calcolato mediante un’analisi multiscala, dovrebbe attestarsi sui 350+/-30 mm invece che raggiungere i 1130+/-480 mm stimati da Sallenger et al. 2012. Di questo problema, però, ho avuto modo di parlare in maniera piuttosto estesa qui (Sallenger et al., 2012)e qui (Scafetta, 2013) per cui, allo scopo di non appesantire eccessivamente il discorso, evito di scendere in ulteriori dettagli.

In questa sede, invece, è mia intenzione approfondire un altro importante risultato conseguito da N. Scafetta, 2013b, ovvero la quantificazione del contributo del forcing solare all’aumento delle temperature superficiali verificatosi nella seconda parte del 20° secolo. Il rapporto IPCC AR4 fissa in un misero 8% il contributo del Sole al riscaldamento globale. Scafetta, 2013b, invece, eliminando le dipendenze lineari che caratterizzano le funzioni prese in considerazione per modellare l’evoluzione del riscaldamento globale, ha potuto accertare che il contributo del forcing solare è stato fortemente sottovalutato: sarebbe del 50% e non dell’8% il contributo del Sole all’aumento stimato di 0,8°C delle temperature superficiali. La questione, però, è molto interessante ed anche piuttosto complessa per cui richiede qualche riflessione preliminare.

I modelli di circolazione generale (GCM) hanno delineato una serie di scenari che, opportunamente valutati dall’IPCC, hanno portato a quantificare il contributo del Sole all’aumento della temperatura superficiale nel periodo 1900-2000 in 0,056°C a fronte di un aumento complessivo della temperatura superficiale di 0,8°C. In un loro studio Benestad e Schmidt, 2009, da ora BS 2009, cercarono di dimostrare che le previsioni dei modelli risultavano essere fondate su solide basi fisiche. Per raggiungere il loro obiettivo BS 2009 hanno adottato un modello di regressione lineare della temperatura superficiale globale che utilizzava 10 funzioni forzanti per definire i parametri della funzione di regressione.

Per ottenere un risultato matematicamente e statisticamente robusto è necessario che le funzioni utilizzate siano linearmente indipendenti, tali, cioè, che per nessuna di esse i coefficienti delle incognite siano derivabili come combinazione lineare dei coefficienti delle incognite delle altre funzioni.

Nel caso di BS 2009, invece, le funzioni utilizzate sono caratterizzate da un andamento monotono del tutto sovrapponibile (in nove casi su dieci) per cui non si può parlare di indipendenza lineare delle stesse. Ciò porta alla conclusione che la regressione multilineare di cui parlano gli autori, in realtà, si basa su presupposti matematici errati e, pertanto, porta a risultati affetti da artefatti analitici che hanno poco senso fisico. Scafetta, 2013b ha analizzato le dieci funzioni utilizzate per costruire il modello di regressione multilineare ed ha individuato una forte correlazione tra le varie funzioni: in qualche caso raggiunge addirittura il 95%. Questa circostanza dimostra che le funzioni utilizzate per il calcolo dei predittori, risultano linearmente dipendenti le une dalle altre e, come si può facilmente intuire, ciò determina una forte amplificazione dell’errore da cui sono affetti i dati di output del modello matematico.

In Scafetta 2013b si dimostra che eliminando le funzioni linearmente dipendenti e calcolando i coefficienti della funzione di regressione sulla base dei dati riferiti al periodo 1980-2003 (più precisi e meno correlati), il contributo del forcing solare al riscaldamento dell’ultima parte del 20° secolo viene fortemente rivalutato e raggiunge i valori già evidenziati in Scafetta e West, 2006a, 2006b, 2007. Il grafico della temperatura così ottenuto, inoltre, riesce a replicare in maniera più fedele di quanto facciano altre funzioni di regressione, le ricostruzioni di temperatura riportate in Moberg et al., 2005; Mann et al., 2008; Ljungqvist, 2010; Christiansen et Ljungqvist, 2012.

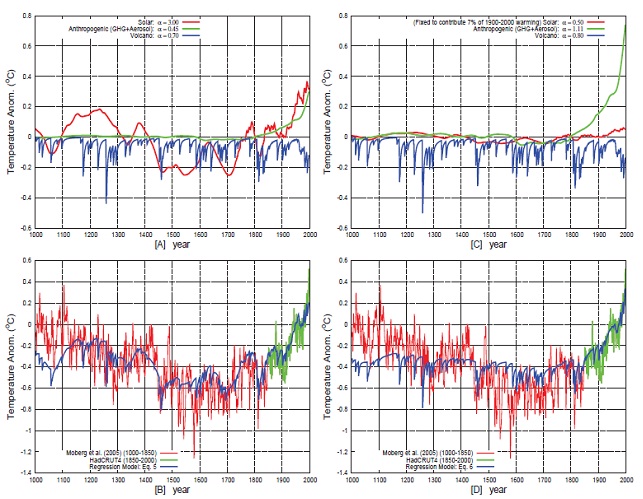
Allo scopo di far meglio comprendere la portata del lavoro del prof. N. Scafetta ho riprodotto la figura 7 di Scafetta 2013b che in originale si trova nel pdf anche scaricabile liberamente dal sito arXiv.org. Nella figura vengono messi a confronto i grafici ottenuti con l’algoritmo implementato da Scafetta (eq. 5 nei grafici) e quelli ottenuti con altre funzioni di regressione (eq. 6 nei grafici).

Ho cercato di riassumere in queste poche righe il lavoro di N. Scafetta limitandomi a mettere in evidenza quelli che a me sono sembrati gli aspetti più interessanti e trascurando quasi del tutto gli interessantissimi particolari più prettamente fisici e matematici dello studio. Essi, per chi fosse interessato, sono facilmente accessibili nel paper originale e, personalmente, ne consiglio la lettura per apprezzare la bontà dell’opera di N. Scafetta, frutto di un lungo periodo di ricerca iniziato anche allo scopo di confutare delle considerazioni contenute nello studio di Benestad e Schmidt, 2009 circa la non ripetibilità di alcuni risultati ottenuti da Scafetta nei primi 10 anni di questo secolo. Con questo paper N. Scafetta dimostra, tra molto altro, che la non ripetibilità dei predetti risultati deriva da errori insiti nelle equazioni utilizzate da Benestad e Schmidt, 2009.