Dopo il post sul lavoro di Akasofu mi sono chiesto se il “non-modello” semi-empirico che ho usato per rappresentare le anomalie medie annuali di NOAA sia accettabile, almeno in termini descrittivi. Ricordo che i dati erano stati approssimati con una retta -i cui parametri derivano dai minimi quadrati lineari- cui si sovrappone una sinusoide con parametri (ampiezza, periodo, fase iniziale) assegnati manualmente, “guardando i dati” e quindi con notevole soggettività. L’altro metodo usato è stato quello di un fit non lineare in cui, fissato il periodo della sinusoide, si cercano quattro parametri. Nel precedente post avevo scritto che ” cambiano leggermente i numeri ma non il concetto complessivo”.
Per cercare di quantificare l’affermazione ho usato il Criterio Informativo Bayesiano (Bayesan Information Criterion o BIC, Schwarz, 1978), ben descritto in un articolo molto citato (Seidel & Lanzante, 2004). Questo articolo è a pagamento e personalmente l’ho trovato con fatica perchè l’Università di Bologna non è abbonata alla sezione D del Journal of Geophysical Research: propongo quindi un riassunto quasi completo (Menne,2006) liberamente disponibile in rete.
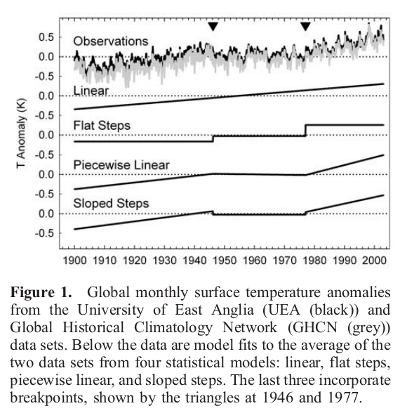
Il metodo BIC parte dalla necessità di descrivere una serie di dati in modo più accurato rispetto alla rappresentazione lineare, e nello stesso tempo ugualmente semplice. Vuole poi trovare un indice statistico in grado di giudicare la bontà di diverse rappresentazioni. Per fare questo viene proposto di dividere la serie in n “segmenti”, definiti da (n-1) break-point scelti opportunamente, ognuno dei quali sia fittato linearmente secondo lo schema mostrato nella Fig.1 di Seidel & Lanzante, 2004 riportata sotto
Per valutare le capacità dei diversi modelli, si usa una modifica del BIC con la grandezza S(q), l’indice che definisce la qualità del fit, calcolata da:
dove q è il numero di parametri usati nel (nei) fit,T e Tmod i dati osservati e calcolati, rispettivamente, n il numero dei dati e Ne il numero efficace (effective) dei dati che dipende dalla funzione di autocorrelazione dei residui a lag=1. Il secondo termine dell’eq.(1) è una “penalità” che rende S(q) più grande al crescere del numero di parametri usati nei fit e del numero efficace dei dati. Il fit risulta tanto migliore quanto minore è il valore di S(q).
Ho applicato il criterio ai dati mensili NOAA fino ad ottobre 2013 (grafici e dati visibili qui) per avere un controllo del metodo, reso più accurato dal maggior numero di dati. Ho poi usato come dati le medie annuali dei dati NOAA fnoa ad agosto 2013 (gli stessi del post precedente) con i 4 break points fissati agli anni 1910, 1945, 1975, 2001, marcati in rosso nella fig.1 (pdf) successiva.
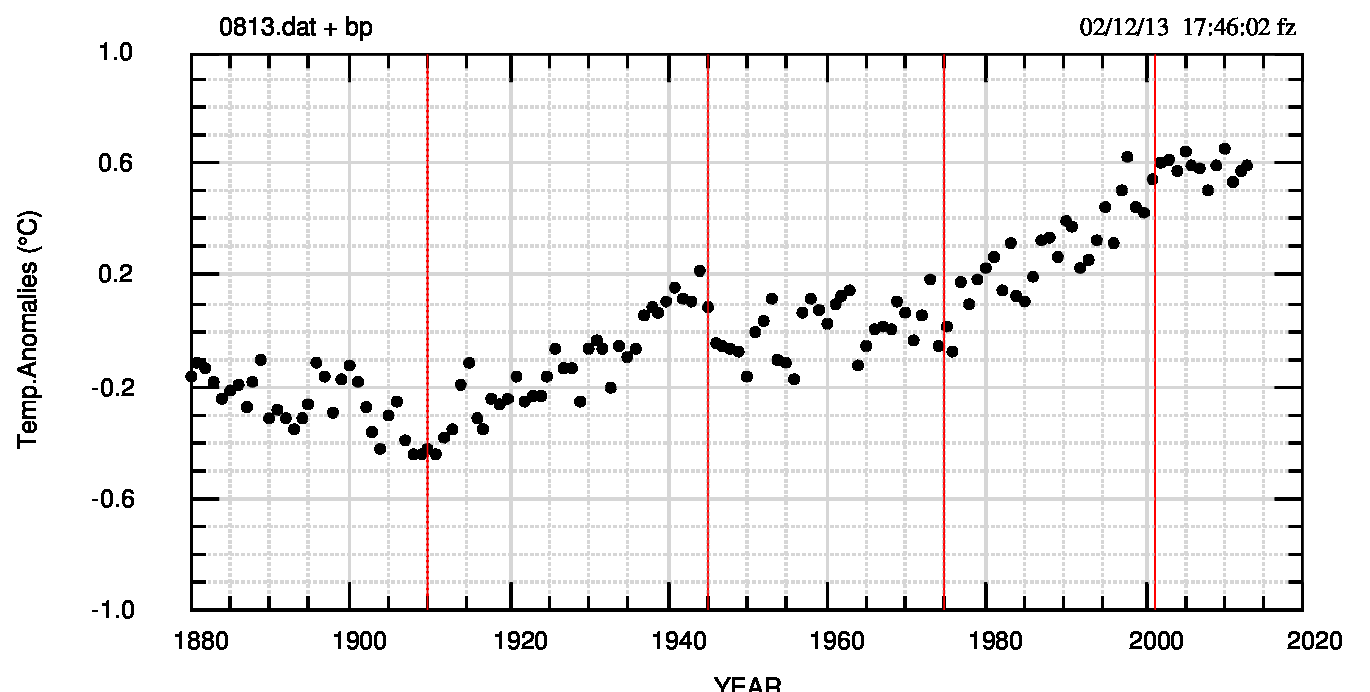
Credo che per questi dati la rappresentazione migliore sia quella detta “piecewise linear” (lineare a tratti, a segmenti) e scelgo di confrontare questo modello con il fit lineare di tutti i dati, con il “non-modello” semi-empirico del post precedente (retta+seno) e con il fit non lineare (retta+seno). Tutti i parametri (tranne quelli semi-empirici che non hanno valori tutti calcolati) sono riportati qui insieme ai valori della funzione di autocorrelazione dei residui, a lag 1 e 2. L’ultimo gruppo di valori, identificato da AFIT08, viene dal fit non lineare e quindi ha una struttura diversa dagli altri gruppi.
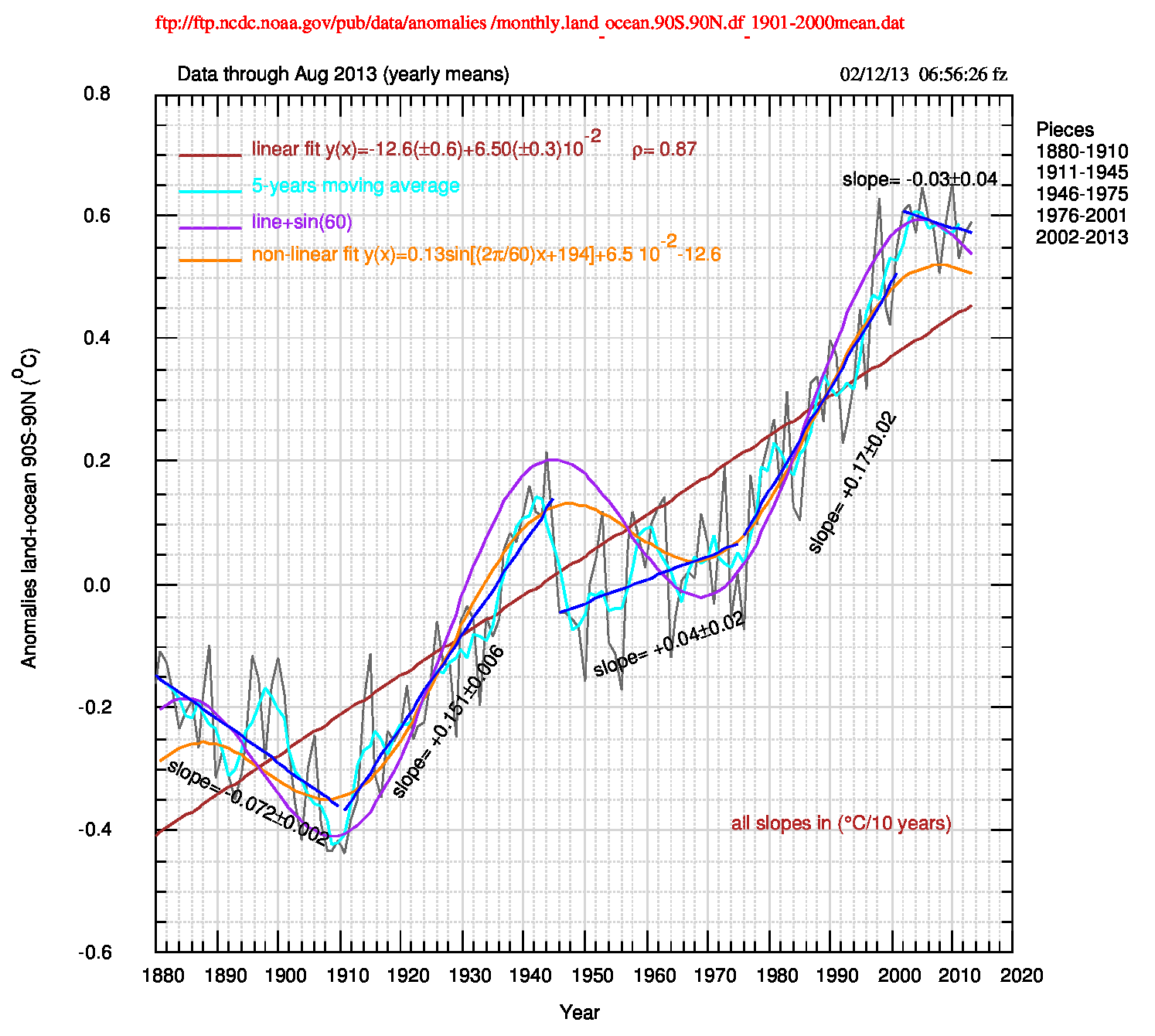
Il grafico successivo (pdf) mostra come si dispongono tutti fit rispetto ai dati osservati.
Il calcolo dell’eq.(1) e di tutte le sue componenti è raccolto nella tabella 1; la seconda parte mostra l’anno e i residui (cioè osservato-calcolato o (o-c)) di tutti i fit. I valori dei segmenti (piecewise o pw) sono stati raggruppati in un unico file dal quale viene calcolato il valore S(q). Seguendo Siegel & Lanzante,2004 o Menne,2006, il valore di q per il modello lineare a tratti (piecewise linear) è 2Nb+2=10, con Nb=4 numero dei break point; nel fit lineare q=2 e in quello non lineare q=4.
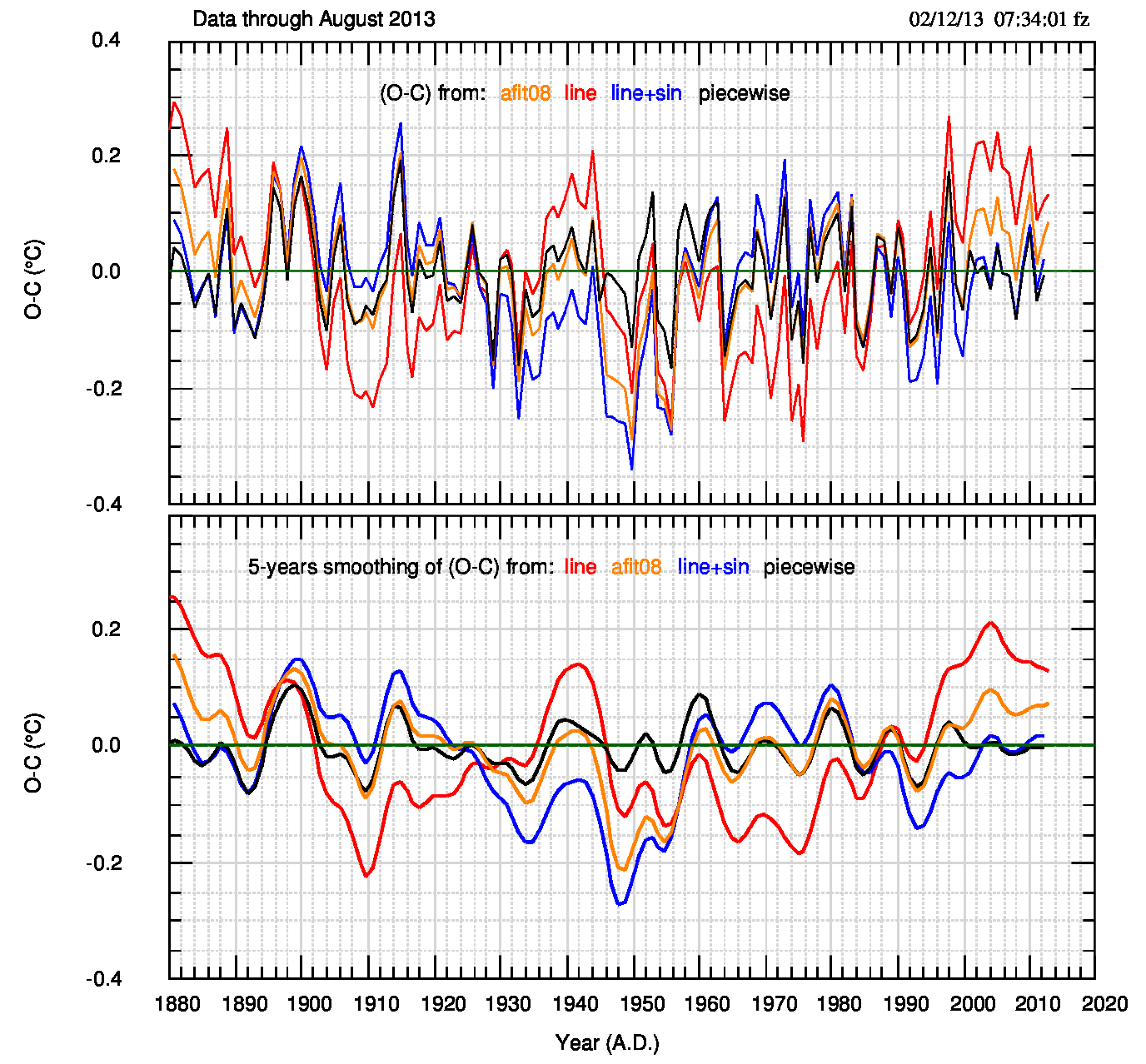
Sia i valori di S(q) che il grafico qui sopra dei residui di Fig.3 (pdf) mostrano chiaramente che il modello lineare a tratti è il migliore, seguito a distanza dal modello non lineare (retta+seno) e dal modello semi-empirico (retta+seno); il modello lineare (retta) è il peggiore, anche se usa il minor numero di parametri.
La “classifica” si vede bene anche nella Fig.4 (pdf).
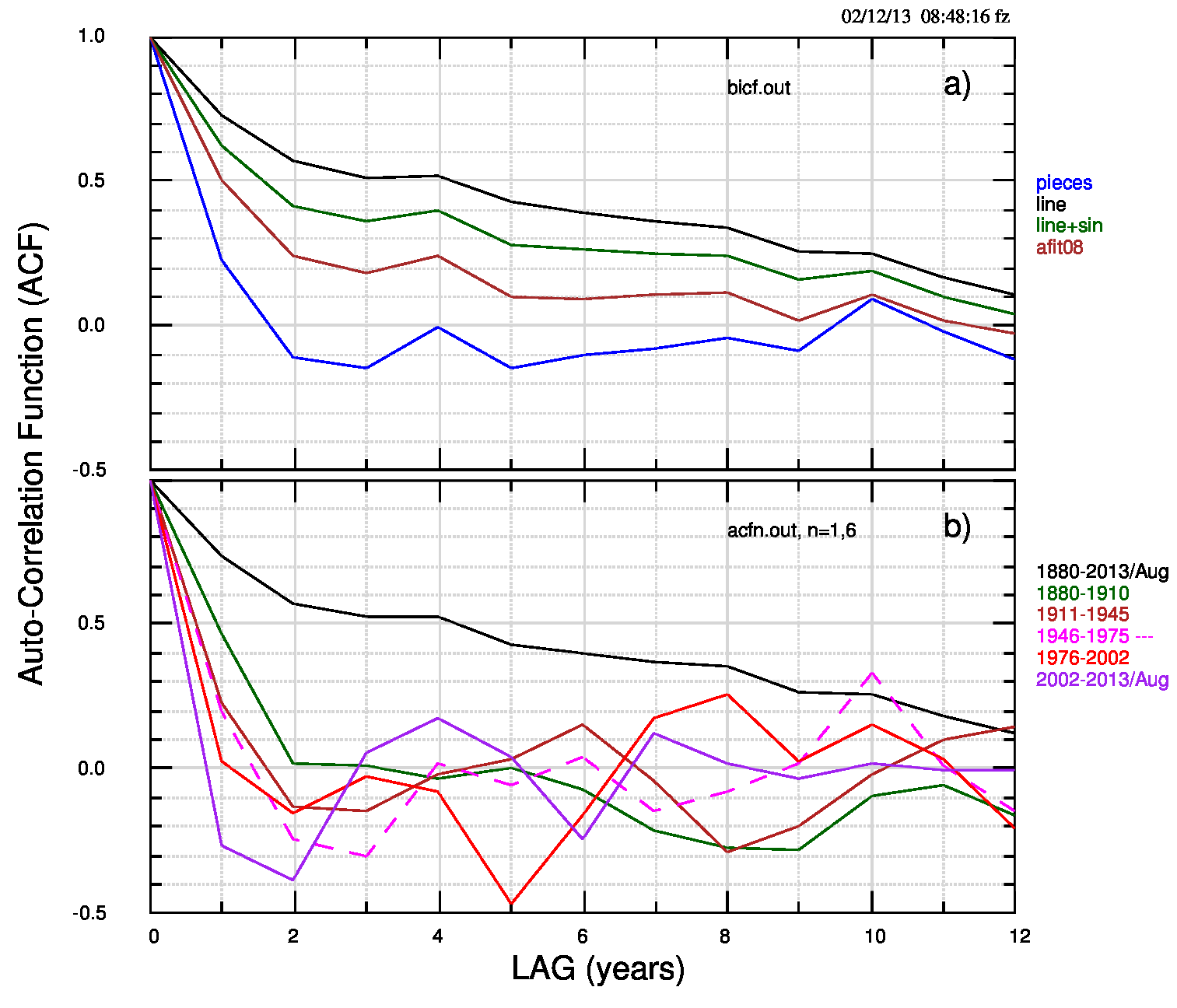
Infatti l’autocorrelazione quasi zero del modello lineare a tratti identifica residui non correlati (o poco correlati) tra loro. Non possiamo parlare di indipendenza tra i residui a lag diverso perché è ben noto che due variabili indipendenti hanno correlazione nulla, mentre la correlazione nulla non implica necessariamente che le variabili siano indipendenti (l’indipendenza -se esiste- va provata in altro modo), ma una bassa correlazione tra i residui è indice di fit migliore.
Il modello lineare a tratti, il migliore in assoluto, in situazioni in cui il numero dei dati nei singoli segmenti è basso potrebbe far pensare ad una influenza preponderante del rumore statistico. Il quinto tratto (2002-2013), composto di 12 valori e unico caso in cui Ne>n, potrebbe essere in questa situazione.
Il conclusione, il modello semi-empirico utilizzato nel post precedente è il peggiore tra quelli esaminati (esclusa la semplice retta) ma, nella sua imprecisione, fornisce almeno un’idea dell’andamento generale delle anomalie di temperatura.
Per finire, una nota divertente: il modello lineare a tratti ha l’insuperabile difetto di essere sotto gli strali di SkS (qui) che accusa gli scettici (del cambiamento climatico, dice: errore blu! semmai dell’AGW) di usare il fit lineare a tratti invece di una sola retta (v. fig.2 e fig.3, sopra per capire il perché). Non mi risulta che Seidel e Lanzante (NOAA al momento della scrittura dell’articolo) e Menne (NOAA, attuale responsabile del dataset, con il quale ho scambiato mail circa un anno fa) siano scettici e non mi risultano strali personalizzati di SkS verso chi per primo ha definito statisticamente il metodo del fit a tratti. Al massimo, “quelli che sbagliano sempre” hanno usato i metodi disponibili e, direi, ben giustificati.
Bibliografia
- Tutti i grafici e i dati numerici sono disponibili qui
- Menne, M.J.: Abrupt global temperature change and the instrumental record , Am.Met.Soc. , 4.3, 86, 2006 (PDF)
- Schwarz G.: Estimating the Dimension of a Model. Ann. Statist., Volume 6, Number 2, 1978, 461-464. PDF al sito del Project Euclid.
- Seidel, D.J., Lanzante,J.R.: An assessment of three alternatives to linear trends for characterizing global atmospheric temperature changes , J. Geophys. Res., 109, D14108, doi:10.1029/2003JD004414, 2004.



“… la rappresentazione sinusoidale (quella con il fit non lineare, non quella semi-empirica) è la migliore dopo il fit a tratti e, anche se si vedono nettamente i break point, i salti improvvisi, la mia natura (le polemiche!) mi porta a vedere meglio transizioni più graduali da uno stato all’altro ….”
.
“Natura non facit saltus” dicevano una volta, poi arrivò la fisica dei quanti e tutto cambiò! 🙂
Commentando il post su Akasofu ebbi modo di constatare che combinando una sinusoide con periodo di 60 anni ed il fit lineare si riusciva a rappresentare in maniera più realistica la distribuzione dei dati dell’archivio NOAA rispetto al solo fit lineare e misi l’accento sul ricorso del periodo circa sessantennale nei vari studi che abbiamo preso in esame nell’ultimo periodo (a breve, per esempio, completerò un post sull’analisi armonica di Scafetta che condividerò con la comunità di CM).
Debbo riconoscere, però, che la rappresentazione per segmenti riesce a dare un’immagine più immediata dei break point ed i coefficienti di correlazione elevatissimi lo dimostrano in modo evidente. Per il resto aspetterò con (im)paziente 🙂 attesa i risultati ottenuti applicando il metodo li L. Mariani alla ricerca oggettiva dei break point nei dati NOAA.
Ciao, Donato.
“Per il resto aspetterò con (im)paziente 🙂 attesa i risultati ottenuti applicando il metodo li L. Mariani alla ricerca oggettiva dei break point nei dati NOAA.”
Mi dispiace, ma non so usare il metodo di Bai e Perron. In compenso, tra ieri sera e questa notte ho preparato un mio sistema per trovare i break point ( http://www.zafzaf.it/clima/bp/bphome.html ).
Non so se è migliore dell’occhio, ma intanto non mi permette di trovare il quarto break point, quello al 2001, riferito alla mancata crescita della temperatura. Ho appena finto e non ho ancora le idee chiare, ma spero con questo di colmare la tua (im)pazienza.
Ciao
Franco
Franco, ho riflettuto sul metodo che hai escogitato per trovare i break point e mi sembra convincente. Ho notato anch’io la mancanza del break point 2001 e concordo con la tua diagnosi: forse è l’occhio che ci inganna. Anch’io continuerò a riflettere sul problema perché è strano che una discontinuità così evidente (ad occhio 🙂 ) non trovi riscontri oggettivi a livello analitico.
Ciao, Donato.
Ho continuato a fare prove, in particolare aumentando il numero dei punti con cui faccio i fit (la risoluzione). Questo ha migliorato la definizione dei BP secondari e ne trovo uno al 2007 (che però non è il 200-2001 che mi aspetterei ad occhio). Ho documentato tutto nel sito di supporto.
Però l’aumento della risoluzione non cambia di una virgola la situazione del 4.o segmento: penso che la colpa sia del metodo che si basa sul cambiamento dei parametri quando, a partire da un segmento, si “sfora” nel segmento successivo. Ora, il 4.o segmento ha un ipotetico 5.o segmento troppo corto per influenzare i parametri del fit. Credo che il metodo non funzioni al bordo della serie dove forse serve l’occhio. Appena uscirà, tra circa una settimana, provero ad usare la serie NOAA di novembre, giusto per allungare il 5.o segmento.
Ciao. Franco
Anch’io, durante questo fine settimana, sono giunto alla tua stessa conclusione: la serie di dati è troppo corta per individuare l’ultimo break point in maniera oggettiva. L’algoritmo di calcolo “vede” i dati successivi all’ultima discontinuità come un continuum con quelli precedenti.
Ciao, Donato.
Hai ragione, Donato, non amo affatto le polemiche. Oltre a SkS (et
similia), però, mi ha dato particolarmente fastidio l’atteggiamento
sprezzante nei confronti di Akasofu -cui ho accennato nel post precedente- e “quanno ce vo’, ce vo'”.
.
Nel post ho verificato anche che la rappresentazione sinusoidale (quella con il fit non lineare, non quella semi-empirica) è la migliore dopo il fit a tratti e, anche se si vedono nettamente i break point, i salti improvvisi, la mia natura (le polemiche!) mi porta a vedere meglio transizioni più graduali da uno stato all’altro.
Per esempio, non ho ancora calcolato i parametri BIC per l’ACE (Accumulated Cyclones Energy, medie annuali) ma la sinusoide (http://www.zafzaf.it/clima/year-large2.pdf ) mi soddisfa e credo che se si dovesse mostrare l’occasione userò ancora questo sistema, confortato dai risultati del post.
C’è anche un’altra fonte di errore di cui devo tenere conto: L. Mariani usa un sistema oggettivo per
determinare la posizione (l’anno) dei break point, io no e li definisco esaminando visualmente i dati. La bontà dei singoli fit dipende allora dalla scelta dei break point: nel post i singoli coefficienti di correlazione sono superiori al 90% per cui questi dubbi sono più teorici che pratici, ma in
generale anche la scelta della posizione dei salti contribuisce ad aumentare l’incertezza del fit a tratti e ad avvicinarlo all’incertezza della sinusoide.
“Per finire, una nota divertente: il modello lineare a tratti ha l’insuperabile difetto di essere sotto gli strali di SkS…”
.
Mentre leggevo l’interessante post di F. Zavatti e apprezzavo la bontà del metodo di rappresentazione dei dati a tratti, pensavo proprio alle bordate polemiche ed irridenti con cui SkS (ed i suoi emuli nostrani 🙂 )bolla le tesi scettiche che suddividono il dataset delle temperature in periodi caratterizzati da momenti di crescita seguiti da momenti di stasi e/o decrescita: definiscono “scala mobile” questa metodica con l’evidente intento di ridicolizzare il tutto.
Conoscendo l’avversione di F. Zavatti per le polemiche, da una parte mi sono sorpreso per la considerazione finale, dall’altra mi sono sorpreso per la “coincidenza” delle mie considerazioni con quelle di F. Zavatti. Particolarmente condivisibile, infine, la differenziazione degli scettici del cambiamento climatico da quelli dell’AGW.
.
A parte lo spunto polemico che, ripeto, condivido, mi sembra che il metodo di rappresentazione dei dati utilizzato da F. Zavatti dia dei risultati estremamente brillanti. Fa piacere notare che autori come Menne, Seidel, Lanzante, ecc. ecc. abbiano giudicato riduttivo (direi, poco rappresentativo) il fit lineare ed abbiano cercato metodiche alternative per rappresentare dati che, di per sé, sono non lineari.
A questo punto è necessaria qualche considerazioni analitica e fisica. Il metodo a tratti mi sembra che colga in modo estremamente efficace dei punti in cui il sistema subisce delle brusche variazioni che, invece, vengono completamente ignorati dalla rappresentazione lineare. Questi punti di variazione dello stato del sistema, a mio modestissimo e personale avviso, dovrebbero essere opportunamente ed accuratamente indagati in quanto sono essi che possono darci delle informazioni circa le cause che influenzano il sistema. Sistema che, sempre personalmente, considero di tipo caotico e caratterizzato da stati di equilibrio che cambiano in corrispondenza dei punti di discontinuità (che, pertanto, assumono anche un significato fisico).
Il lavoro di F. Zavatti, in altre parole, mi conferma ancora di più in queste mie convinzioni.
Ciao, Donato.
Il richiamo al compianto climatologo Reinhard Bohm dello ZAMG fatto da Franco Zavatti ci rammenta il fatto, scontato fin che si vuole, che dietro alle serie storiche c’è tanta umanità.
Una volta si trattava di un’umanità fatta di persone che salivano 3 volte al giorno (8, 14, 19) le torri degli osservatori e che compilavano enormi registri dei quali periodicamente tiravano a mano le somme.
Oggi è tutto diverso e molto, forse troppo, è stato automatizzato. Tuttavia il fattore umano continua ad essere l’elemento centrale per dar senso compiuto ai numeri. Speriamo che continui ad esserlo anche in futuro.
PS: in rete è ad esempio disponibile il resoconto di una conferenza dal titolo “La ricostruzione del clima con le antiche serie di misura” tenuta da Bohm a Torino:
http://personalpages.to.infn.it/~cassardo/pensieri/2008_04_07.html
E’ vero. A questo proposito ho il mio personale ricordo del Sig. Orgeo Fusi Pecci, custode della Specola Universitaria di Bologna, che per alcune decine d’anni ha fatto quanto dice L.Mariani: 4-5 piani di scala a chiocciola (3 volte al giorno) per salire sul terrazzo della torre a prendere i dati meteo dalla “casetta”, dal pluviometro e dall’eliofanografo e poi compilare i “libroni” delle osservazioni. E, dopo la sua pensione, il servizio più che secolare è stato chiuso.
Come piccolo contributo al dibattito segnalo che due anni orsono, seguendo le orme di Seidel e Lanzante, ho operato il confronto fra i 3 modelli (flat step, sloped step e lineare) con riferimento alle temperature di 171 stazioni europee e con lo scopo di individuare 2 sottoperiodi omogenei a cui applicare un’analisi delle risorse termiche per le piante coltivate (per inciso i sottoperiodi individuati sono stati 1951-87 e 1988-2010).
I risultati, pubblicati nel lavoro qui sotto, indicano che lo sloped step è il migliore, seguito dal flat step e dal modello lineare.
L Mariani, S G Parisi, Cola G, Failla O (2012). Climate change in Europe and effects on thermal resources for crops. International Journal of Biometeorology, ISSN: 0020-7128, doi: 10.1007/s00484-012-0528-8
Noto con stupore che l’articolo è disponibile gratuitamente qui: http://air.unimi.it/bitstream/2434/177434/2/Mariani%20et%20al.%2010.1007_s00484-012-0528-8%5B1%5D.pdf
Lavoro molto interessante che mostra la potenza del BIC e del fit lineare a
tratti, quando opportunamente trattato dal punto di vista statistico. Sono
stato impressionato dalla capacità di mettere in evidenza (fig.5b) il salto
climatico del 1987, nato in Atlantico e trasferitosi verso
l’Europa continentale, man mano indebolendosi. Noto anche (a meno di interpretazioni errate) la
possibilità di mettere bene in evidenza lo spostamento verso nord (fig.6) delle
colture dei gruppi II e III dopo il 1987. Ringrazio Luigi Mariani per aver
messo a disposizione l’articolo e senz’altro accoppio il suo stupore al
nostro piacere per aver potuto disporre del full text.
Ora permettetemi due parole al di fuori dell’argomento che stiamo trattando:
la fig. 1 dell’articolo (la mappa delle stazioni usate) mi ha fatto tornare
in mente Reinhard Bohm del Servizio Meteo Austriaco (ZAMG) con cui ho avuto
un inteso scambio di mail tra l’8 agosto e il 13 settembre 2012. Da lui ho
ricevuto molto materiale dettagliato delle stazioni del dataset HISTALP e
chiari segni di amicizia. Solo dopo un anno ho saputo che era deceduto
pochi giorni dopo il nostro ultimo contatto, il 5 ottobre 2012, e vorrei
approfittare di questa occasione per ricordarlo con affetto e stima.