Riassunto: Commento la tendenza ad eliminare l’influenza solare sul clima terreste, considerando le ciclicità derivate dagli spettri dei dataset climatici come frutto di combinazioni inattendibili di fattori “altri” rispetto al Sole. Come sempre, non trovo appropriati gli aspetti più estremi di questo genere di diatribe.
Premessa
Fra il 13 e il 15 marzo 2018 sono apparsi su WUWT due articoli che riflettono la lotta che si è generata su quel sito tra i cosiddetti “ciclisti”, coloro che credono nelle ciclicità derivate dagli spettri di innumerevoli dataset disponibili, e cercano di interpretarle, e coloro che ritengono queste periodicità poco più (o anche poco meno) che artefatti generati dal trattamento dei dati, come ad esempio l’uso di dati detti “stacked”, cioè la media di più serie, o la scelta selettiva di particolari sezioni dei dataset) o dall’uso di questa o quella tecnica di analisi spettrale (di questi tempi vanno molto di moda le tecniche che permettono di osservare l’evoluzione temporale dei picchi spettrali, tipo wavelet o CEEMD che spesso vengono contrapposte a tecniche “statiche” tipo Mem, Lomb-Scargle, MTM).
Personalmente, come i lettori di CM sanno anche troppo bene, ho prodotto e continuo a produrre spettri (Mem e Lomb, ma anche MTM, Redfit, Wavelets) di ogni dataset climatico con cui ho a che fare, proponendo per i massimi spettrali interpretazioni legate alla circolazione atmosferica e marina e ad influenze esterne legate al sistema solare e a fenomeni galattici come i raggi cosmici. In questo seguo con interesse i lavori di Nicola Scafetta (anche lui oggetto della suddetta guerra) con i cui spettri mi sono confrontato all’inizio per verificare la bontà dei miei risultati. Mi considero quindi un “ciclista”, ma con il tempo ho acquisito una specie di riluttanza alla scelta dei massimi “significativi” secondo criteri dettati da livelli di significatività che ritengo in buona parte arbitrari. Infatti gli spettri variano spesso in ampiezza (o potenza) e definire la “realtà” di un massimo spettrale in base all’altezza del picco (in quel momento) mi sembra riduttivo. Preferisco definire la presenza di un massimo in base alla sua frequenza di apparizione in più dataset o in più osservazioni dello stesso dataset. Quindi “ciclista” sì, ma un po’ strano. Poi non gradisco filtrare i dati, normalizzarli, standardizzarli, riempiere i loro “buchi”, ecc. prima di calcolarne lo spettro: e quindi ancora più strano nel panorama attuale.
Tornando al discorso, Javier ha pubblicato un articolo su WUWT in cui deriva e propone varie ciclicità legate al Sole, in particolare il ciclo di Eddy di circa 960 anni, e in generale la relazione tra clima e variabilità solare.
Prontamente, nel giro di due giorni, Javier viene attaccato da Willis Eschenbach (campione anticiclista, insieme a Leif Svaalgard) che si propone di smontare la presunta influenza solare, utilizzando la CEEMD e mostrando come i massimi spettrali siano un artefatto dell’uso dei dati “stacked” (medie su 4 dataset). Mostra che usando i 4 dataset separatamente il massimo di circa 960 anni scompare o almeno si distribuisce su un arco temporale di circa 1000-1500 anni, diventando di fatto inesistente. E poi fa notare che i massimi indicati da Javier (e anche altri) esistono solo in particolari periodi dell’Olocene e non in altri, sottolineando questo aspetto come se avesse qualche particolare significato (che per me è sconosciuto). Il carattere “ruvido” di Eschenbach lo ha poi portato a considerazioni personali nei confronti di Javier (perchè usa uno pseudonimo e non il suo vero nome) francamente poco apprezzabili.
Analisi spettrale delle 4 serie di Bond et al., 2001
Non tutto ciò che scrive Eschenbach mi sembra sbagliato: anche per me l’uso della media dei 4 dataset disponibili genera confusione e andrebbe evitato. Infatti propongo di seguito l’analisi delle 4 serie separatamente.
Ma anche ciò che scrive Javier, in particolare la sua figura 2 e le conseguenze che se ne possono trarre, non mi trova d’accordo. Circa un anno fa avevo analizzato i carotaggi provenienti dalla grotta di Dongge che coprono un periodo di circa 340 mila anni (tra 300 e 640 ka) e che sembrano interessanti per le ciclicità di lungo periodo, meno per quelle attorno a 1000-1500 anni. La figura 2 di Javier mostra uno spettro Lomb molto pulito, che sembra il risultato di processi di smussamento (usa i dati stacked) e/o di selezione di una particolare parte del dataset. Per confronto, la figura 1 (pdf) presenta la parte finale del mio spettro Lomb calcolato su tutta l’estensione temporale e sul dataset più esteso (SB-14).
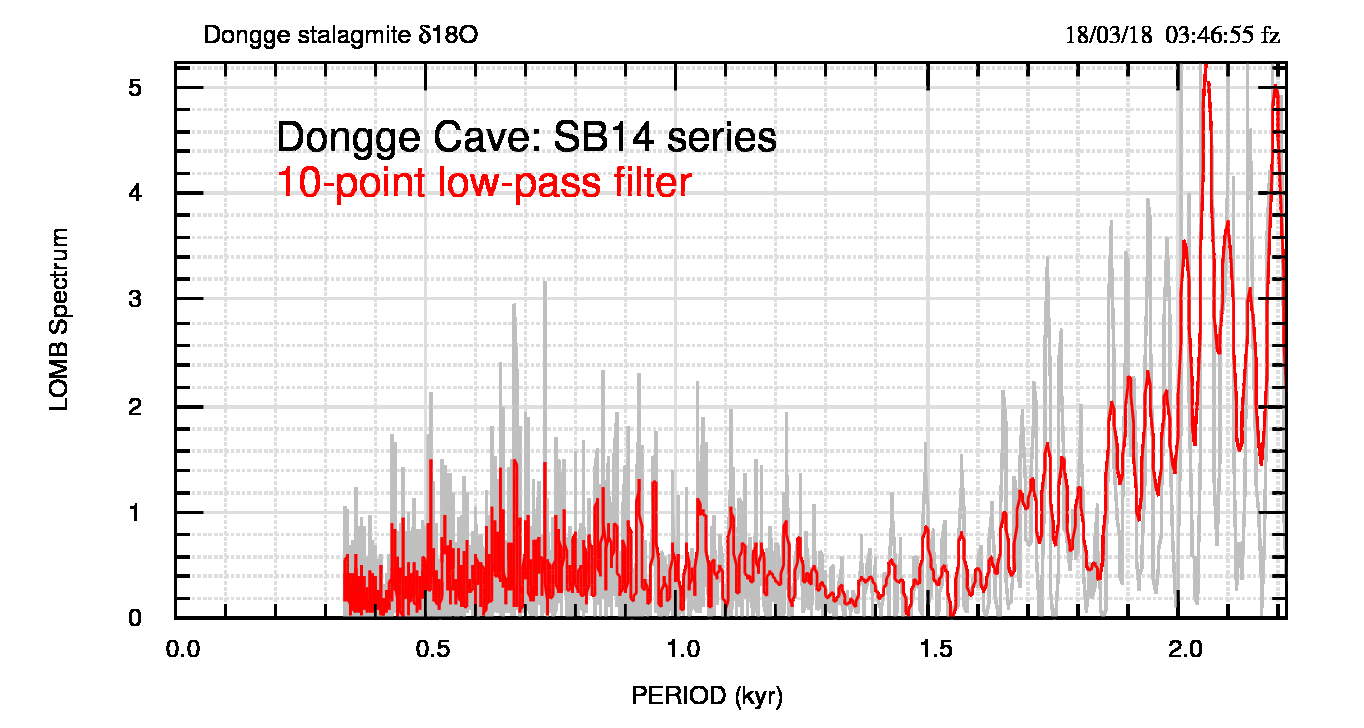
Non mi sembra che tra 900 e 1500 anni sia possibile identificare qualche massimo spettrale, in particolare quelli indicati da Javier. Non ho graficato gli spettri degli altri dataset disponibili per Dongge ma essendo più brevi di questo si configurano come un possibile cherry picking.
Anche Debret et al., 2007 si rifà ai dati pubblicati da Bond et al., 2001, in particolare nella figura 2 che riproduco sotto.

Qui Debret mostra l’esistenza dei massimi di circa 950 anni e di, forse, 1500 anni; quest’ultimo appare molto più vago dell’altro considerando anche la presenza di picchi superiori a 2400 anni che poco hanno a che fare con 1500 anni.
Di seguito, l’analisi spettrale di una delle serie di Bond et al., 2001, anche con la correzione della persistenza, preceduta da una tabella che permette di identificare le serie, chiamate qui e in Eschenbach in modi diversi. Per i grafici delle altre serie, rimando al sito di supporto.
| Nome Ufficiale | Eschenbach | FZ | FZ-Comp |
| MC52V29191 HSG | Hematite | bondi | bond-1 |
| MC52V29191 glass | Glass#1 | bondii | bond-2 |
| MC21GGC22 glass | Glass#2 | bondiii | bond-3 |
| MC21GGC22 det carb | Detrital Carb | bondiv | bond-4 |
In questa serie si vede, per la prima volta, il limite connesso con il mio sistema (http://www.climatemonitor.it/?p=47359 ) di calcolo del coefficiente di Hurst, H, basato sulla funzione di autocorrelazione a lag 1 [acf(1)]. il valore di acf(1) è alto e fornisce un alto valore di H corretto, mentre si vede bene che l’acf per alti lag fornisce un valore limite che tende mediamente a zero, come dovrebbe essere per una buona correzione. Il valore di H riportato in blu in figura 3 (pdf) non è quindi attendibile.
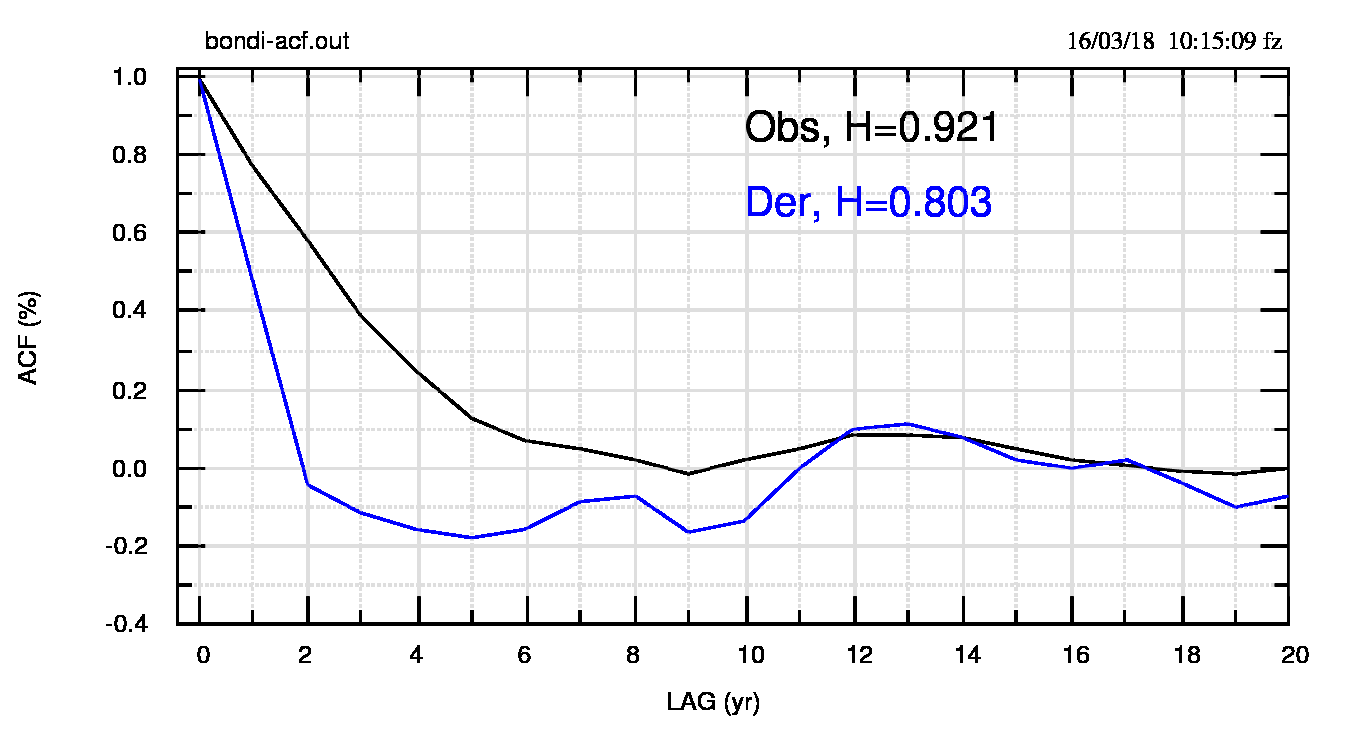
I valori e lo spettro LOMB della serie osservata e di quella corretta con la derivata numerica può essere confrontato in figura 4 (pdf) e in figura 5 (pdf).
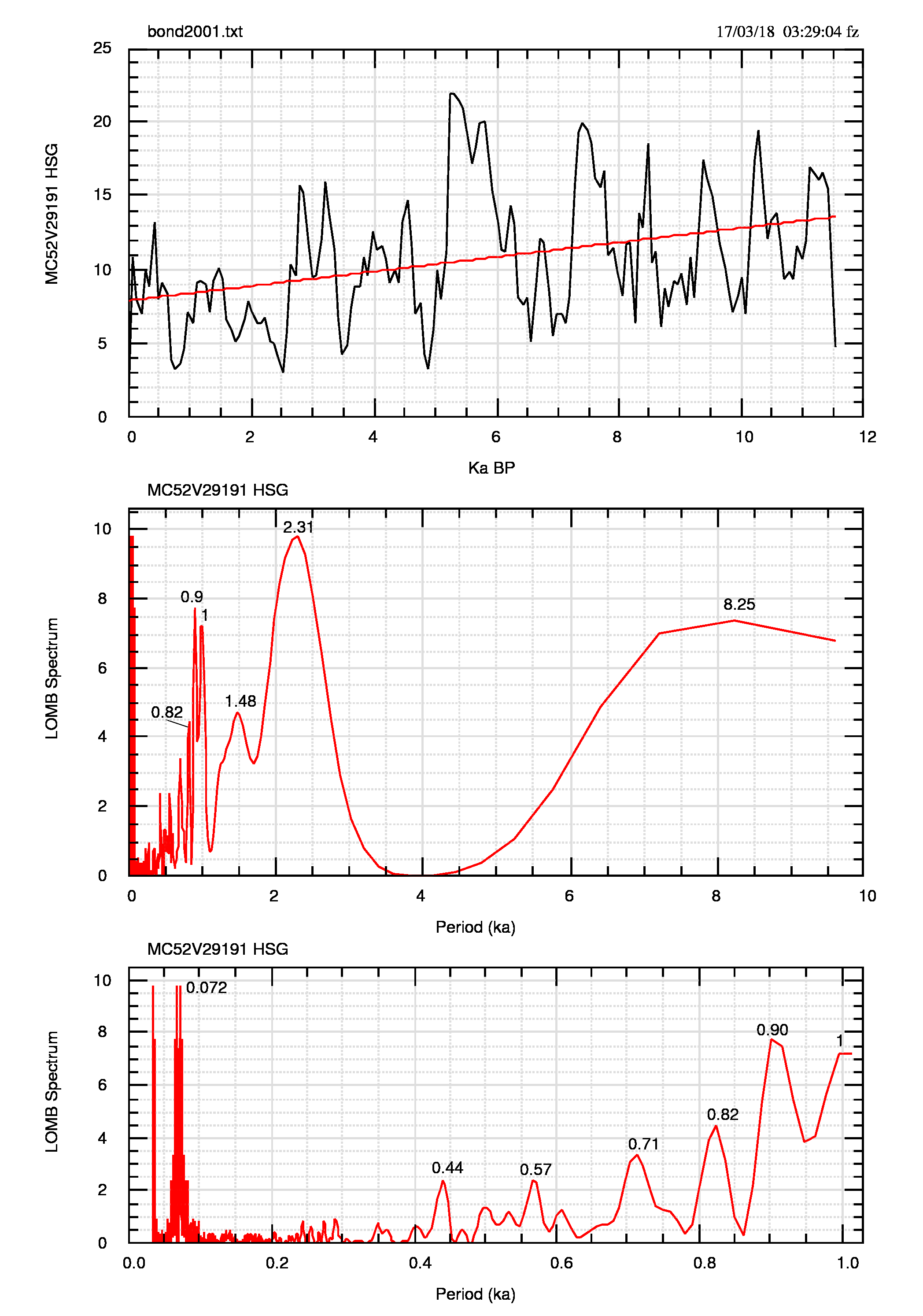
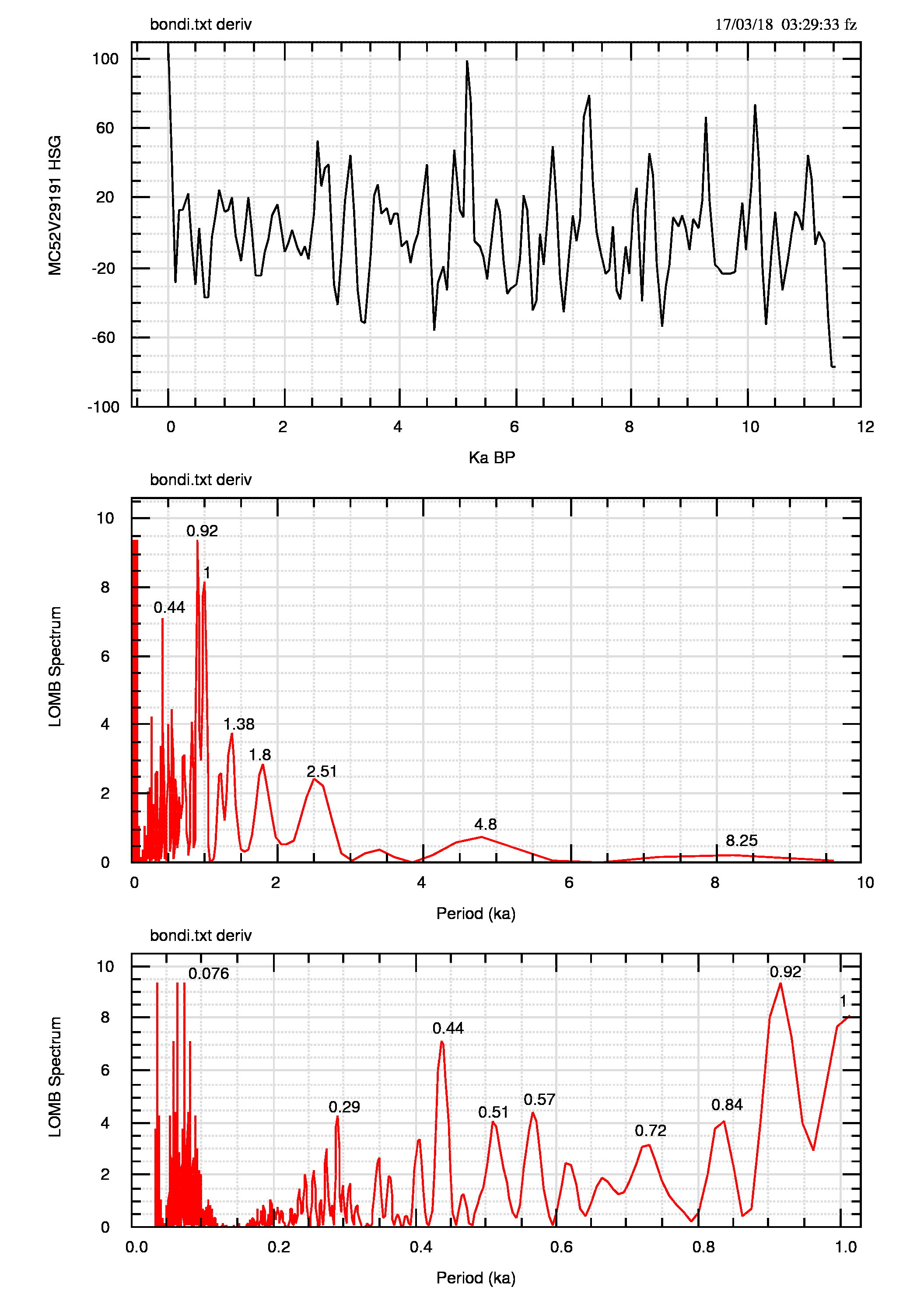
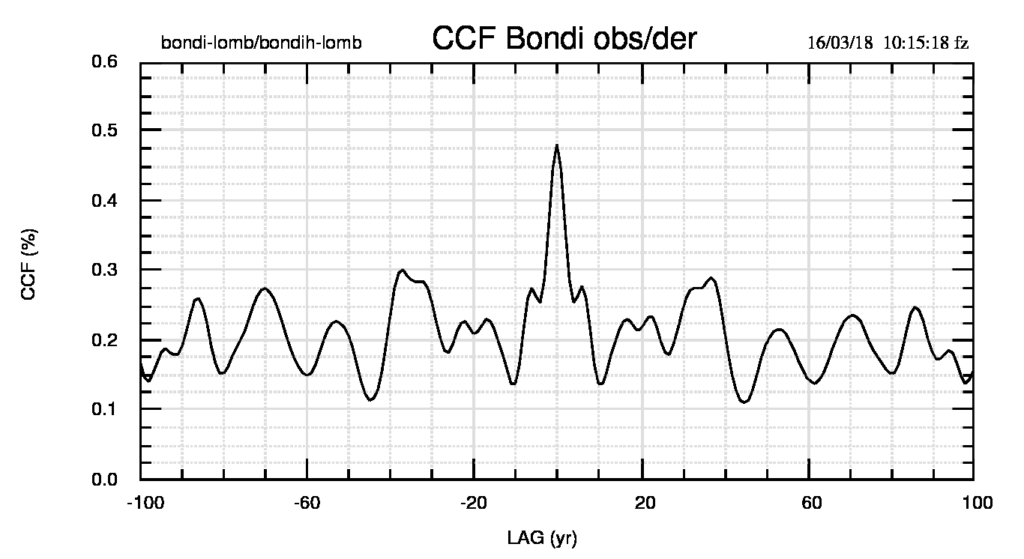
Un confronto diretto tra gli spettri può essere fatto anche usando la figura 6 che mostra, per osservato e derivata, nella tabella di sinistra, i massimi spettrali corrispondenti (i dati tra parentesi esistono, in genere sono deboli e non sono stati identificati con un valore numerico del periodo), oppure con l’adiacente Funzione di Cross-Correlazione (CCF, grafico a destra) da cui si vede che le due serie sono esattamente allineate -il massimo di CCF è a lag 0- e che non ci sono, se non molto deboli, altre posizioni reciproche (cioè a lag≠0) in cui la correlazione ha valori poco diversi da zero. Il grafico ci dice anche che la correlazione di Pearson, cioè la ccf a lag 0, è 0.539, valore sufficientemente elevato per due serie che dovrebbero o potrebbero essere diverse e non correlate.
|
|
Il confronto fra gli spettri mostra ancora una volta come la memoria a lungo termine abbia agito sui periodi più lunghi, rendendoli più potenti nei dati osservati e più deboli nei dati corretti per la persistenza, ma ancora presenti (perchè escluderli, seguendo un’analisi di significatività, dato che non sono semplicemente rumore?).
Come detto sopra, riportare la stessa analisi per tutte le serie sarebbe troppo lungo (tutto è disponibile nel sito di supporto) ma è interessante osservare come si comporta l’insieme dei massimi spettrale delle quattro serie, sia osservate che corrette.
Il confronto viene evidenziato in figura 7 (pdf).
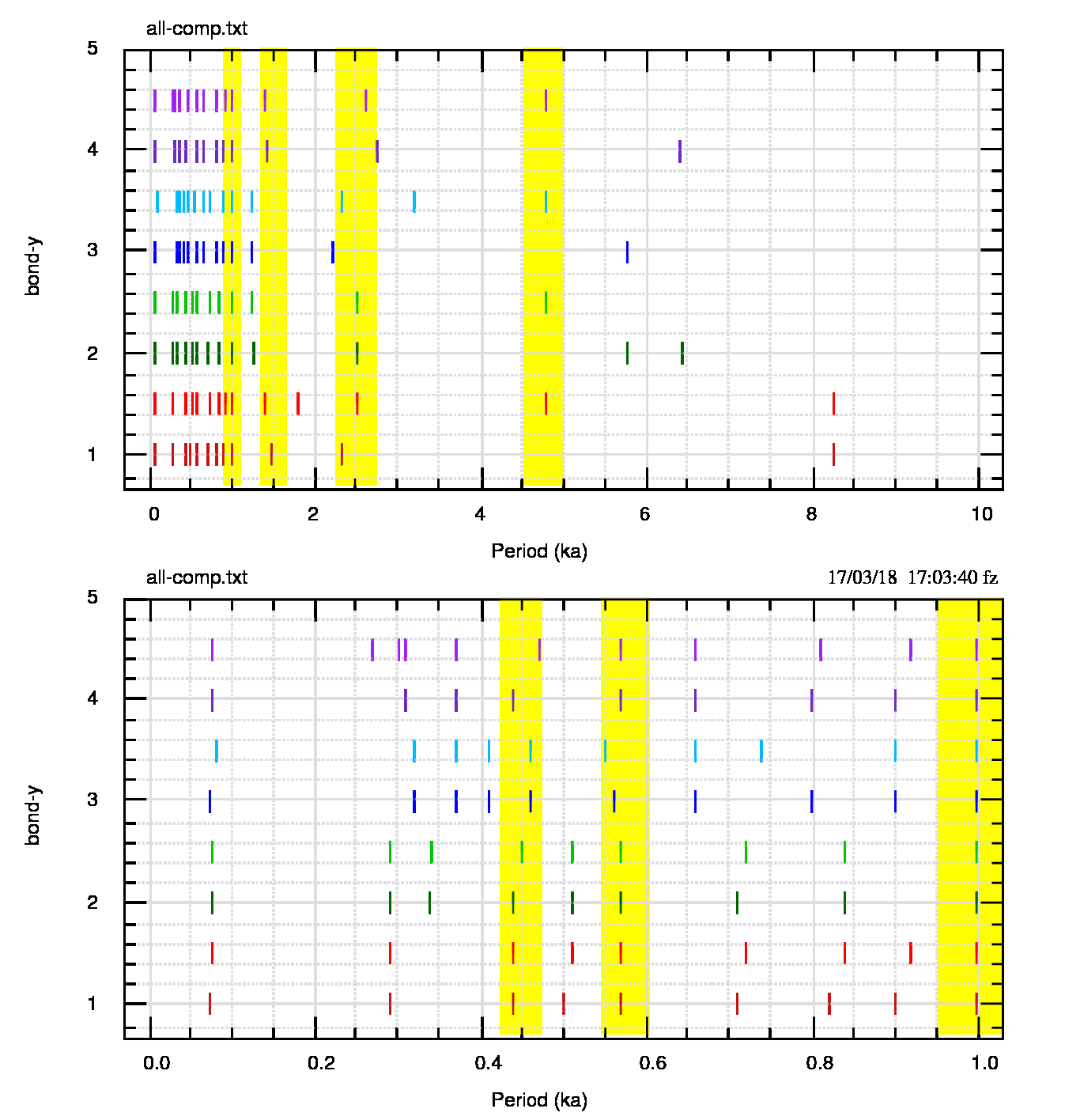
Dalla figura emergono alcuni aspetti:
- Non sono presenti periodi superiori a 5000 anni, se non in maniera sporadica e solo nei dati osservati (non in quelli corretti). Solo la serie bondi, osservata e corretta, mostra un periodo di 8200 anni, ma da sola non può costituire una caratteristica generale.
- Il periodo centrato a 4750 anni ha una caratteristica particolare: esiste per tutte le serie, solo nei dati corretti dalla persistenza. Non sono presenti nelle vicinanze periodi dei dati osservati. Mi piacerebbe pensare ad un merito della correzione per la memoria a lungo termine, ma questo richiederà ulteriori approfondimenti. Credo che gli spettri dei dati corretti siano più attendibili di quelli osservati per cui considero reale questo periodo.
- Il periodo di 2500 anni è presente in tutti i dati corretti e, in modo più defilato, nei dati osservati tranne bondiii. Per quanto posso dire, il periodo è reale.
- Il periodo centrato a 1500 anni (oggetto del lavoro di Debret et al., 2007) è presente solo in bondi e bondiv, osservato e corretto. Ammesso (e per nulla concesso) che qui abbia senso parlare di statistica, il 50% dei casi lascia la aperta la questione dell’esistenza di questo massimo che pure è stato osservato nei dati proxy per il Miocene (23-5 Ma fa, ma non in quelli per l’Olocene) da Kern et al., 2012.
- Il periodo di circa 1000 anni è presente in tutte le serie (osservate e corrette). Mi sembra difficile poter affermare (come Eschenbach) che questo periodo sia un artefatto.
- La considerazione precedente vale anche per i periodi centrati a 550 e a 450 anni.
- I periodi minori di 450 anni si presentano in “ordine sparso” e non so bene come considerarli. A prima vista sembrerebbero “firme” spettrali dovute all’una o all’altra serie e quindi situazioni “locali” nel tempo e nello spazio che non fanno pensare a qualcosa di comune.
- il periodo centrato a 72 anni è comune a tutte le serie e conduce a legami con AMO/NAO. Però il passo dei dati è di 70 anni e un periodo di 72 anni, per quanto la sua esistenza sia possibile, autorizza a più di un sospetto: questo è il motivo per cui non è stato evidenziato da una banda gialla.
References
- Gerard Bond, Bernd Kromer, Juerg Beer, Raimund Muscheler, Michael N. Evans, William Showers, Sharon Hoffmann, Rusty Lotti-Bond, Irka Hajdas, Georges Bonani: Persistent Solar Influence on North Atlantic Climate During the Holocene , Science, 294, 2130-2136, 2001. doi:10.1126/science.1065680
- M. Debret, V. Bout-Roumazeilles, F. Grousset, M. De McManus, N. Massei, D. Sebag, J.-R. Petit, Y. Copard and A. Trentesaux: The origin of the 1500-year climate cycles in H North-Atlantic records , Clim.Past, 3, 569-575, 2007. full text (download PDF)
- A.K. Kern, M. Harzhauser, W.E. Piller, O. Mandic, A. Soliman: Strong evidence for the influence of solar cycles on a Late Miocene lake system revealed by biotic and abiotic proxies , Palaeogeography, Palaeoclimatology, Palaeoecology, 329-330, 124-136,2012.
DOI: 10.1016/j.palaeo.2012.02.023
| Tutti i grafici e i dati, iniziali e derivati, relativi a questo post si trovano nel sito di supporto qui |

@Luca Rocca
No, per carità, non ho visto nessuna critica che, in ogni caso, non sarebbe stata fuori luogo.
Quello che ricordo dei battimenti è la marcia dei soldati sul ponte a una frequenza tale da riprendere la frequenza propria del ponte e farlo oscillare con ampiezza amplificata fino a farlo crollare. Per questo, in caso di battimenti mi aspettavo ampiezze maggiori nel segnale.
Però continuo a non capire: il segnale esaminato ha una estensione temporale di 11700 anni e se il periodo di 8200 anni può sembrare troppo lungo rispetto all’intervallo di osservazione (ma è pur sempre più di un periodo), tutti gli altri sono determinati da quasi tre periodi completi (4700 anni), fino a 26 periodi (450 anni); a parte 8200 anni, che non ho neanche preso in considerazione, dagli altri periodi non mi aspetto interazioni con l’estensione delle serie tali da generare battimenti. Però devo riconoscere che non conosco bene l’argomento. Franco
Potrebbe provare a passare un filtro passa alti in modo da escludere fenomeni noti come le ciclicità solari e le oscillazioni del baricentro causate dal’ allineamento dei giganti gassosi, che hanno periodi sotto i cento anni . Compararlo con i risultati ottenuti e verificare se il segnale millenario subisce o meno delle modifiche
Grazie per il suggerimento: proverò senz’altro ad usare un filtro passa-alto e a vedere cosa succede. Franco
Caro Franco, è da parecchio tempo che non seguo più WUWT, ma ricordo ancora i violenti scontri tra W. Eschenbach e L. Svaalgard e gli autori e/o sostenitori degli articoli (soggetti a revisione tra pari e non) che individuavano periodicità nelle serie climatiche. Questi scontri non mi sono mai piaciuti né nei toni, né nei contenuti.
Non è il caso, però , di soffermarsi più di tanto sulle polemiche di WUWT, in quanto il tuo articolo merita alcune considerazioni.
.
Concordo con te circa il fatto che se alcuni periodi compaiono in più serie che, tra l’altro, sono indipendenti le une dalle altre, non si può parlare di coincidenza o di artefatto di calcolo, come abitualmente fanno coloro che contestano in toto le periodicità desunte dalle serie di temperature.
Io sostengo da tempo che il sistema climatico è un sistema non lineare, ma non dimentico che anche questi sistemi presentano delle regolarità e che, molto probabilmente, vengono stabilizzati nello spazio delle fasi da attrattori, di cui ancora non conosciamo appieno le caratteristiche fisiche e matematiche.
I periodi che tu hai individuato in tante serie climatiche, testimoniano queste regolarità e non possiamo negarle a priori, visto che non siamo in grado di individuarne le cause fisiche.
Dal mio punto di vista, sembra corretto prenderne atto e aspettare di conoscerne le cause, se ci sono.
.
Per concludere una considerazione sul tuo modo di calcolare il coefficiente di Hurst o, per essere più precisi, eliminare la persistenza delle serie climatologiche. Ho riflettuto parecchio sulla derivazione delle serie numeriche e mi sono convinto che funziona. La derivazione è, in ultima analisi, una differenza (limite del rapporto incrementale, per essere precisi), per cui se facciamo la differenza tra due valori della funzione, eliminiamo la parte costante della stessa, cioè la parte che determina autocorrelazione, ovvero persistenza. Nel caso delle serie di Bond sembra che essa funzioni poco in quanto il coefficiente di Hurst si abbassa, ma non raggiunge il valore auspicabile, ovvero un valore intorno a 0,5.
Perché? Non so rispondere, per adesso suggerirei di considerare la cosa accidentale e proseguire su questa strada. Se il problema dovesse ripresentarsi, sarà opportuno pensarci un po’ su.
Ciao, Donato.
Caro Donato,
non posso che essere d’accordo con quanto scrivi, anche nella parte più antipatica, quella delle polemiche sui “ciclisti”.
Credo che non si possa fare altro che registrare quanto si osserva e si calcola, cercando di capire dove possano essere gli errori e le cose da correggere man mano che si va avanti. A titolo personale preferisco lasciare ad altri le “verità vere” e le affermazioni assolute.
Il mio modo di calcolare l’esponente di Hurst H è certamente sbagliato perché uso un solo termine (il primo) di una serie all’infinito (a voler essere buoni si può dire che il mio valore è un limite superiore). Il sistema funziona, nel senso che fornisce un’indicazione quasi attendibile del valore di H, se il primo termine, cioè acf(1), è zero o negativo. Se, come nel caso delle serie di Bond usate qui, il termine è (ampiamente) positivo bisognerebbe seguire la definizione originale della formula che uso in modo approssimato e valutare la convergenza a zero della funzione di autocorrelazione per grandi lag (e questa è una cosa che le serie di Bond fanno dopo la correzione con la derivata). Ma ormai ho capito che, almeno per gli spettri, il valore di H conta poco (è importante nella compravendita di azioni): chi conta è la differenza o derivata della serie perché questa operazione riduce la persistenza anche se H sembra non confermarlo.
Ho tentato di calcolare H secondo le regole (R/S) definite da Hurst ma ho fatto tre tentativi a vuoto di riprodurre i valori calcolati da altri, anche se ogni volta credevo di rispettare le sequenze giuste, non sempre chiarissime. A questo punto ho deciso di smettere e di lasciar decantare per un po’ l’argomento per riprenderlo tra qualche tempo.
Però non potrò più smettere di calcolare e confrontare tra loro gli spettri osservato e corretto. Ciao. Franco
ho l’impressione che a frequenze così basse sia facile confondere un battimento con un fenomeno fisico. o astronomico
Sì, certo, è possibile, ma non mi è chiaro a quale situazione ti riferisci: i periodi che mostro -credibili o meno- coprono un intervallo che va da 8200 a 72 anni e in gran parte li considero poco o per nulla attendibili. Poi, non sono sicuro di vedere negli spettri delle amplificazioni attribuibili a battimenti. Franco
Per favore non la veda come una critica al suo lavoro, non era mia intenzione.
Io vedo questo lavoro come il trattamento di un segnale periodico (mi occupo di acustica), e noto che il periodo di analisi è molto breve rispetto al segnale che si cerca e che è altamente probabile che un battimento di frequenze superiori vada ad alterare la misura . In sintesi lo stesso fenomeno può’ essere provocato da una ciclicità astronomica o dalla combinazione di più eventi coincidenti. Non scendo nel dettaglio ma questo tipo di analisi mi danno l’impressione di avere un margine di errore molto alto