In articoli precedenti (qui, qui, qui e qui) della serie che ha cercato situazioni climatiche in cui si manifestasse il massimo spettrale di 18.6 anni (ciclo della linea dei nodi lunare), si è messo in evidenza come in alcuni casi di misure del livello marino questo massimo fosse presente. D’altra parte l’influenza lunare sulle maree è indiscutibile e quindi dobbiamo aspettarci che anche l’oscillazione della linea dei nodi lasci qualche traccia nelle serie di misure di marea.
Mario Giuliacci, nel suo libro Se non ci fosse la Luna… (Mursia, 1997), scrive, a pag.43:
il ciclo di 18 anni nell’inclinazione dell’orbita lunare sarebbe responsabile anche di una periodica oscillazione del livello degli oceani. E’ questa la conclusione a cui sono giunti nel 1965 due climatologi russi, Maksimov e Smirnov, i quali hanno accertato che quando la luna si spinge verso la massima declinazione di 28°, il Medio Atlantico tende a sollevarsi di quasi 13 centimetri rispetto alla posizione di minima declinazione di 18° raggiunta 9 anni dopo”,
da cui deriva che il dislivello che si crea tra 30-40° di latitudine e le latitudini maggiori spinge enormi quantità di acqua temperata verso le calotte polari, portando con sé importanti conseguenze.
Nella convinzione che questo tipo di influenza lunare possa manifestarsi nello spettro dei livelli marini, ho approfittato di una selezione di serie mareografiche di PSMSL (Permanent Service for Mean Sea Level), pubblicata da Willis Eschenbach nel 2017 con altri scopi e basata sul fatto che le serie iniziassero almeno dal 1950, che contenessero almeno 50 anni di dati e meno del 5% di dati mancanti. Le scelte hanno condotto alle 63 serie mareografiche (dalle originali 1505) che uso in questo lavoro.
I dati erano stati originariamente suddivisi in 6 “contenitori” contenenti 10 serie ognuno, più un settimo con solo 3 serie; ho mantenuto questa suddivisione a 7 e ho calcolato, per ognuna, lo spettro Lomb delle serie. Un esempio degli spettri della prima suddivisione è in figura 1; le altre sono nel sito di supporto dove sono disponibili anche i grafici delle serie mareografiche.
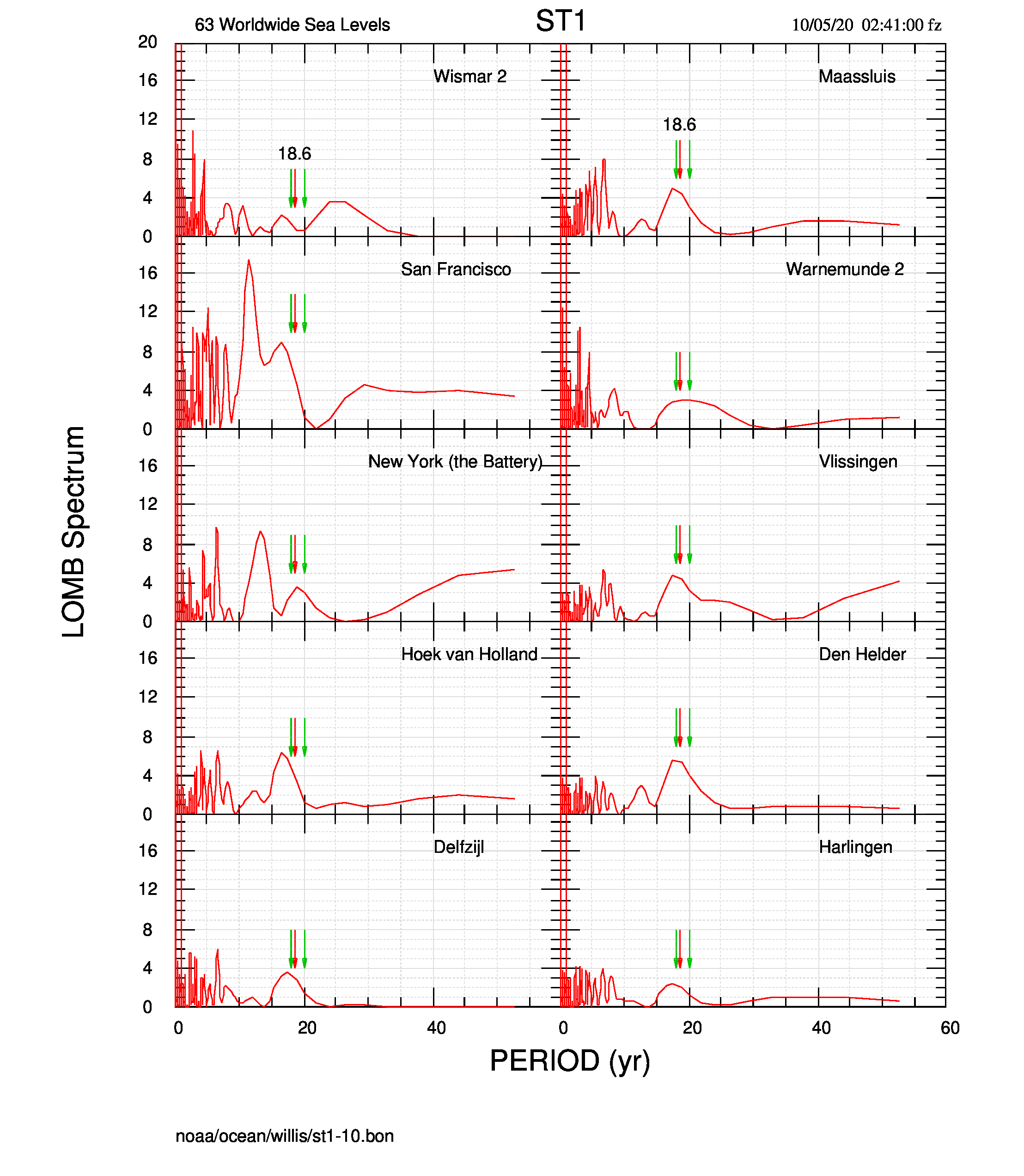
Il risultato complessivo è che il massimo a 18.6 anni, rispetto ai 7 gruppi di dati e senza tenere conto delle frecce verdi, si trova in 29 casi e non si trova in 34 casi, secondo lo schema della tabella successiva:
| Gruppo | Si | No |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 6 | 4 |
| 3 | 3 | 7 |
| 4 | 6 | 4 |
| 5 | 7 | 3 |
| 6 | 2 | 8 |
| 7 | 0 | 3 |
I “Si” presentano 4 casi incerti e i “No” 8 casi incerti, entrambi indicati con “~” nell’ultima colonna di tabella 3. Tenere in considerazione le frecce verdi, cioè un intervallo maggiore, cambia alcuni (pochi) numeri ma non la sostanza di quanto si osserva: grosso modo metà degli spettri sembra risentire dell’influenza lunare e metà no, troppo poco per poter affermare che il ciclo nodale della Luna influenza il livello del mare e troppo poco per poter affermare il contrario.
Un tentativo non sistematico di osservare negli spettri le super- e sub-armoniche di 18.6, quindi 37.2, 9.3, 6.2, 4.65 anni, ha mostrato che si osservano in pochi casi valori vicini a 6.2 e in qualche caso in più valori vicini a 4.65 anni, senza una reale possibilità di utilizzare questi periodi per poter dire, come ad esempio fanno Serikh e Sonechkin (2017) per El Nino, che sono le armoniche ad avere importanza.
In tabella 1 le stazioni mareografiche sono state ordinate secondo la latitudine, per verificare se l’influenza della Luna cambia con questa coordinata, come esplicitamente afferma Mario Giuliacci nel suo libro, e sono state divise in tre fasce arbitrarie di latitudine con i risultati mostrati nella tabella che segue.
| Lat | #dati | Si | No | ~ |
|---|---|---|---|---|
| 65°÷51° | 25 | 15 | 10 | 8 |
| 50°÷36° | 22 | 8 | 14 | 1 |
| 35°÷-34° | 16 | 6 | 10 | 3 |
Ancora una volta i risultati sono poco significativi e, in particolare nella fascia centrale, il massimo spettrale di 18.6 anni è presente in poco più della metà dei casi, poco per affermazioni statisticamente significative. Solo nella fascia nord il “Si” è il 50% più del “No”.
Cercando il lavoro di Maksimov e Smirnov citato da Giuliacci, mi sono imbattuto (tramite Google Books, v. bibliografia) in Parker et al., 1995 che pubblica le due figure che riporto di seguito, tese a dimostrare la presenza del ciclo lunare sia nella serie del pescato di halibut del Pacifico che nella temperatura dell’aria a Sitka (Alaska).

Non posso dire nulla sulla serie del pescato di halibut, ma nella sezione 6 dei dati mareografici presentati qui, si trova lo spettro della serie del livello marino di Sitka che contiene il picco lunare. Anche la sovrapposizione di figura 2 tra questa serie e una sinusoide di periodo 18.6 sembra sufficientemente accurata, ma non rende l’idea di un fenomeno generalizzato. La bibliografia di Parker (1995) riporta l’indicazione di una serie di lavori di Robert G. Currie che, dal 1987 al 1992 ha mostrato come il ciclo lunare di 18.6 anni sia presente in vari record climatici, dalla temperatura dell’aria alla precipitazione. Royer (1993) discute il massimo lunare connesso alla variabilità oceanica ad alte latitudini.
Conclusioni
Le conclusioni possibili, a mio parere, sono incerte: il massimo spettrale di 18.6 anni si osserva in circa la metà dei 63 casi trattati qui e la dipendenza dalla latitudine della stazione mareografica è discutibile. In particolare è difficile vedere in questi dati il livello più alto del medio Atlantico che riversa verso le regioni polari acqua temperata. Anche se alcuni lavori hanno in passato dimostrato che stazioni ad alta latitudine presentano, negli spettri di varie variabili climatiche, il massimo a 18.6 anni, nelle stazioni di media latitudine è più raro vedere questo picco nello spettro e non capisco come possa non essere presente alle medie latitudini e, in qualche modo, generarsi alle alte.
La discrepanza tra quanto derivato da molti ricercatori, dagli anni ’70 in poi, ma anche informazioni di tipo storico lo esprimono, e quanto trovo io qui, mi fa pensare che forse l’intervallo 18-20 anni che ho scelto come limite estremo del massimo “lunare” sia troppo conservativo, data l’ampia dispersione dei dati osservati, ma non voglio forzare la mano estendendolo in un modo che mi sembra arbitrario. I grafici e i valori numerici degli spettri sono disponibili e i lettori potranno autonomamente decidere se la mia scelta è stata corretta.
Alla fin fine osservo che quello delle piogge e della nuvolosità è l’unico fenomeno meteo-climatico in cui la presenza del picco spettrale di 18.6 (18-20) anni è significativa e, se di influenza lunare si tratta, si può dire che sia sistematica nelle piogge, con qualche “incursione” nel livello marino e in altre variabili climatiche (qui una lista).
Bibliografia
- Parker K.S., Royer T.C. and Deriso R.B.: High-latitude climate forcing and tidal mixing by the 18.6-year lunar nodal cycle and low-frequency recruitment trends in Pacific halibut (Hippoglossus stenolepis), in Climate change and northern fish population, Ed. R.J.Beamish, Can. Spec. Publ. Fish. Aquat.Sci., 121, 1995.
- Royer T.C.: High‐latitude oceanic variability associated with the 18.6‐year nodal tide, JGR, 98, C3, 4639-4644, 1993. https://doi.org/10.1029/92JC02750
- I.V. Serykh and D.M. Sonechkin: Manifestations of Motions of the Earth’s Pole in the El Niño–Southern Oscillation Rhythms , Doklady Earth Sciences, 472,p2, 256-259,2017. https://doi.org/0.1134/S1028334X17020301
- Google Books per la ricerca di Maksimov & Smirnov, 1965. (anche l’articolo di Parker et al. 1995)
| Tutto il materiale relativo a questo post si trova nel sito di supporto |


Le mie conoscenze di astronomia sono drammaticamente scarse ma mi ricordo che per la conservazione del momento angolare la rotazione della Terra si oppone all’ effetto mareale della Luna causandone il progressivo decadimento dell’orbita.
Dato che il momento è massimo all’ equatore e zero ai poli coinciderebbe con l’effetto descritto nel suo articolo. Bisognerebbe verificare con qualcuno che ha fatto qualcosa di più del corso di geografia astronomica della V liceo
Il “qualcuno che ha fatto qualcosa di più del corso di geografia astronomica della V liceo” sono io. Sono laureato in Astronomia e ho lavorato 40 anni al
Dipartimento di Astronomia di Bologna, anche se non mi sono occupato di pianeti e orbite.
Il fenomeno descritto è reale ma non ha influenza sulla presenza del massimo a 18.6 anni. Se ne avesse i massimi “lunari” sarebbero molto frequenti (nel senso che sarebbero presenti in molte serie) attorno all’equatore e quasinulli vicino ai poli, il che non è, come appare dalla serie di post sull’argomento che hanno spaziato in varie aree geografiche.
Come ho sottolineato nella risposta a Donato, nel mare di Bering la presenza del massimo a 18.6 anni dovrebbe essere quasi nulla quando in realtà è
presente, poche volte ma non come evento eccezionale.
La Terra ha effetto sulla Luna, ma anche la Luna e il Sole ne hanno sulla Terra: questo effetto si vede ad esempio nel LOD (length of day) la cui serie mostra, seppur debolmente, un picco a 19.2 anni. Nel grafico che accludo, c’è anche la SST che, oltre allo stesso massimo di LOD, mostra un forte picco a 9.2 anni (~18.6/2). Franco.
Immagine allegata
Caro Franco,
la lettura del tuo articolo mi ha un po’ sconfortato. Il titolo mi aveva entusiasmato, ma man mano che andavo avanti nella lettura, mi rendevo conto che la probabilità che il ciclo delle precessioni nodali, potesse avere un ruolo nelle oscillazioni del livello del mare a bassa frequenza, diminuivano sempre di più. Alla fine devo ammettere che la probabilità che il ciclo nodale lunare sia in grado di modulare il livello medio del mare è la stessa che lanciare una monetina e sperare che esca croce: 1/2.
Statisticamente bisogna riconoscere che il comportamento delle stazioni mareografiche da te analizzato, è di tipo stocastico rispetto al ciclo di periodo 18-20 anni.
Non è una conclusione che mi conforta, ma questo è il bello della matematica: toglie i dubbi ed affievolisce le certezze. 🙂
.
Alla luce dei tuoi risultati aumenta il mio scetticismo anche nei confronti dello studio di Zaccagnino e colleghi. Pur essendo diversi i meccanismi di azione delle maree lunisolari a bassa frequenza sulle placche tettoniche, infatti, le criticità evidenziate nel mio post di commento all’articolo, ne escono rafforzate. E’ pur vero che la viscosità dell’astenosfera consente di accumulare le tensioni e che il periodo delle precessioni nodali è in risonanza con il tempo di Maxwell della zona di disaccoppiamento relativamente alle sollecitazioni tangenziali, ma si tratta di cose tutte da dimostrare.
.
In tutto ciò mi resta un dubbio molto forte. Come può il ciclo dei nodi, influenzare l’andamento delle piogge, visto che non è in grado di modulare l’andamento del livello medio del mare e, quindi, gli scambi termici tra zone diverse dell’oceano, come ipotizzato da Giuliacci e dagli studi da lui citati?
E quale meccanismo fisico gli consente di modulare le piogge, visto che i suoi effetti non sono riscontrabili su ENSO?
Ciao, Donato.
Caro Donato,
… e tutto il tuo pessimismo deriva dalla “poderosa” presenza del picco in circa il 50% dei mareografi. Sto finendo un lavoro su serie di pesca, biologiche e
climatico-atmosferiche nel mare di Bering e trovo solo il 3% delle serie climatiche con un picco tra 18 e 20 anni; se dettaglio, sono 15 casi di cui 9 hanno 18.6 anni e 6 18 anni (il ciclo dei nodi e il ciclo degli apsidi
della Luna, rispettivamente). Nelle serie di pesca e in quelle biologiche, nulla (zero casi).
Puoi quindi immaginare il mio pessimismo, ma, come scrivi tu, cerchiamo di fare le cose al meglio e poi prendiamo ciò che viene.
Come hai visto, da questo post ho cominciato a scrivere “lunare”, tra virgolette proprio perché non riesco ad immaginare una universalità così poco universale e non trovo (certo per mia ignoranza) una relazione tra la posizione della Luna e la presenza o assenza del massimo “lunare”; anzi ho trovato un lavoro (Treloar,2002, doi:10.1002/joc.783) dove, nelle conclusioni si può leggere “ Coupling the 6.00 and 1.1273 year cycles produces phase-shifted cycles with intervals of 18.02 years. There are ten consecutive 18.02 year events followed by a 5.82 year phase shift, followed by another ten events separated by 18.02 years, and so on.
Averaging this behaviour over ten intervals, the mean interval is 18.6 years, and so we seem to connect the saros (more accurately 18.030 years in length) with the 18.6 year lunar nodical cycle“.
Troppi anni che entrano in gioco, troppe cifre decimali e troppe mescolanze per i miei gusti: sempre più immagino tentativi (sicuramente onesti) per far
tornare le cose …
Comincio a pensare a possibili coincidenze di periodi e a cause diverse dalla Luna, ma per ora aspetto e tenterò di fare altre verifiche.
Per il lavoro di Zaccagnino & C, sto ancora cercando di capire se chiedere i dati o lasciare stare, e i dubbi non aiutano.
E, certo, come fa la Luna a modulare le piogge se non riesce a modulare le caratteristiche degli oceani, diciamo in generale dei fluidi? Ciao. Franco