L’esponente di Hurst e gli spettri (Parte II) – Altre applicazioni

Livello del lago Vittoria
Questo argomento è stato trattato su CM qui. La serie del livello del lago Vittoria ha un esponente di Hurst H=0.962 ed è adatta alla procedura descritta nel post precedente con la differenza che adesso i dati non sono a passo costante. Il calcolo delle differenze deve essere fatto per unità di ascissa (la differenza tra due valori non ha molto senso se non viene rapportata all’intervallo su cui è stata calcolata) e quindi, in pratica, si calcola il rapporto incrementale Δy/Δx, ovvero la derivata numerica.

Ho però voluto verificare anche il comportamento delle differenze assolute e nei nomi dei programmi di calcolo e delle versioni pdf dei grafici sono presenti i termini “deriv” o “der” oppure “diff”, ad indicare i due casi. Intanto noto che H_deriv=0.781 e H_diff=0.683; quindi l’uso delle differenze/derivate non è così efficace da annullare la persistenza. Entrambe le tecniche la riducono (lavorano meglio le differenze) ma i valori di H sono ancora alti. Penso comunque che l’analisi spettrale dovrebbe (o potrebbe) risentire positivamente della diminuzione di H rispetto ai dati originali. In fig.6 (pdf) il confronto tra le ACF.

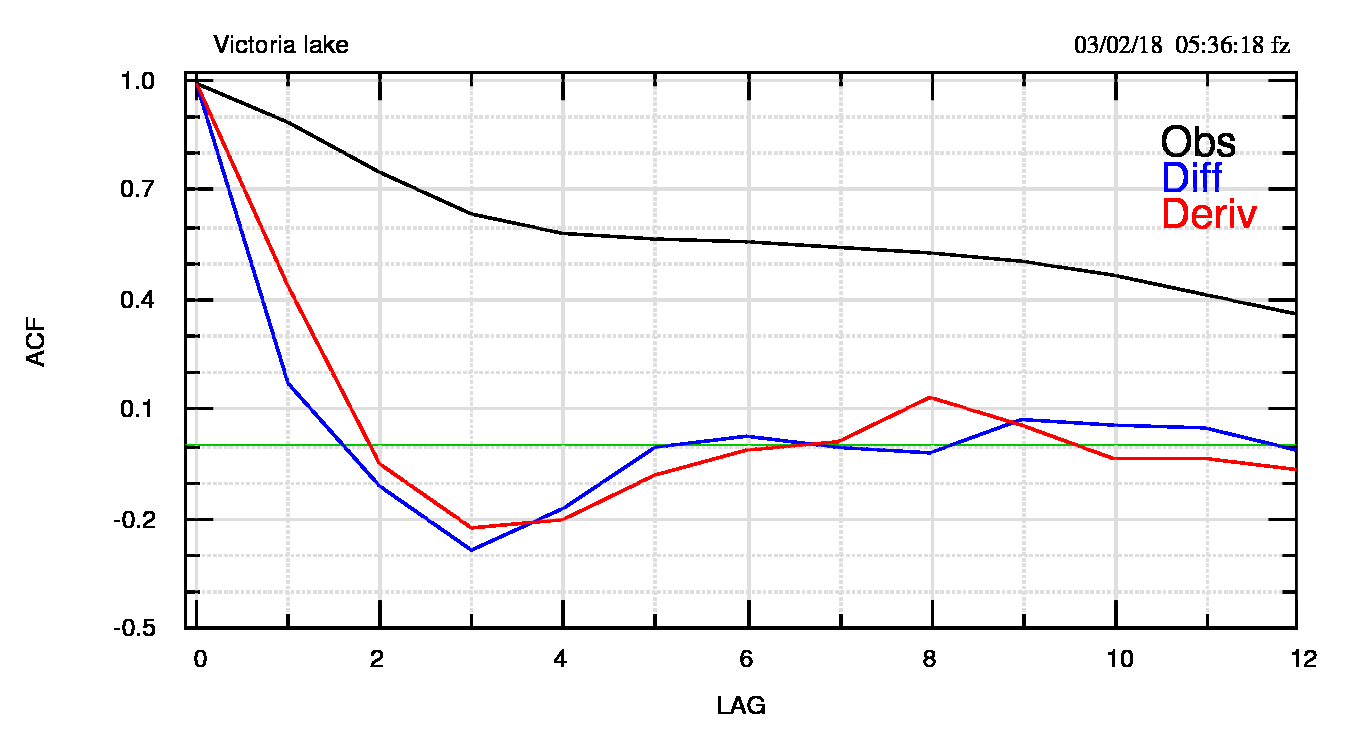
Nelle figure successive presento l’equivalente di figura 4 e di figura 5 per il lago Vittoria e il confronto con i dati originali.

Dalla figura 6 e dalle figure 7 (pdf) e 8 (pdf) emerge che, oltre ad una decisa diminuzione della persistenza, gli spettri sono simili tra loro ed entrambi diversi dallo spettro dei dati originali di figura 9 (pdf), in particolare per le basse frequenze (periodi più lunghi).

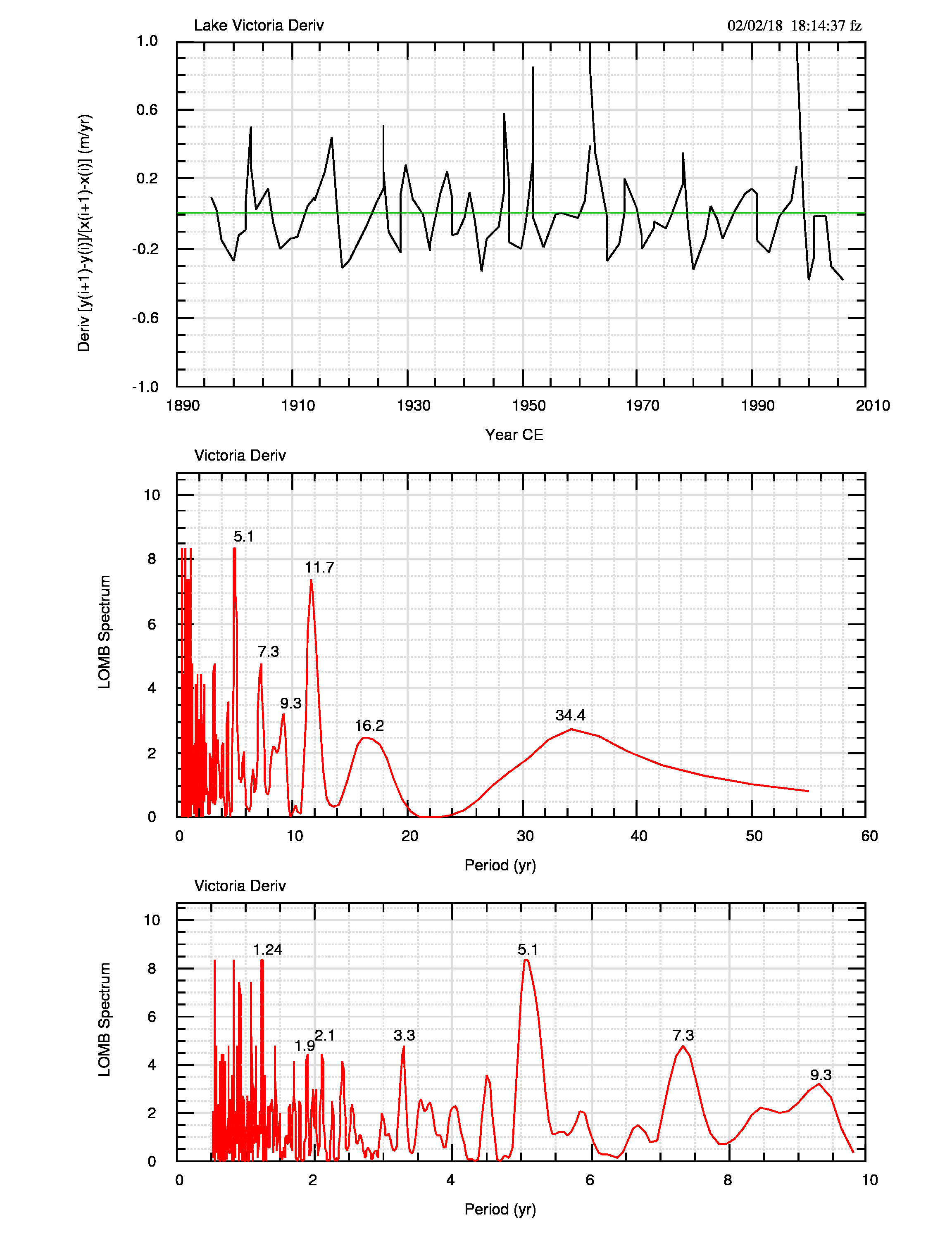
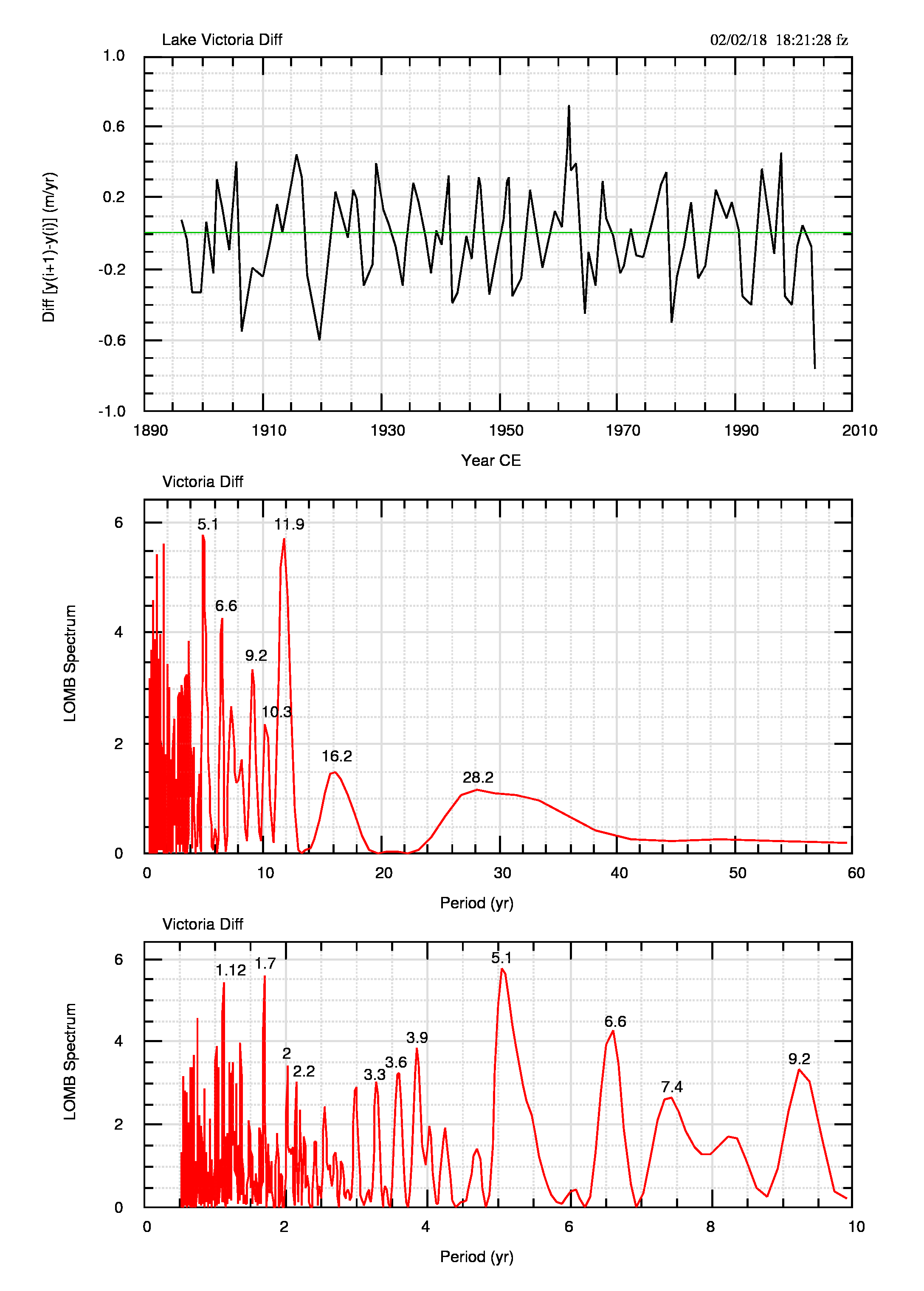
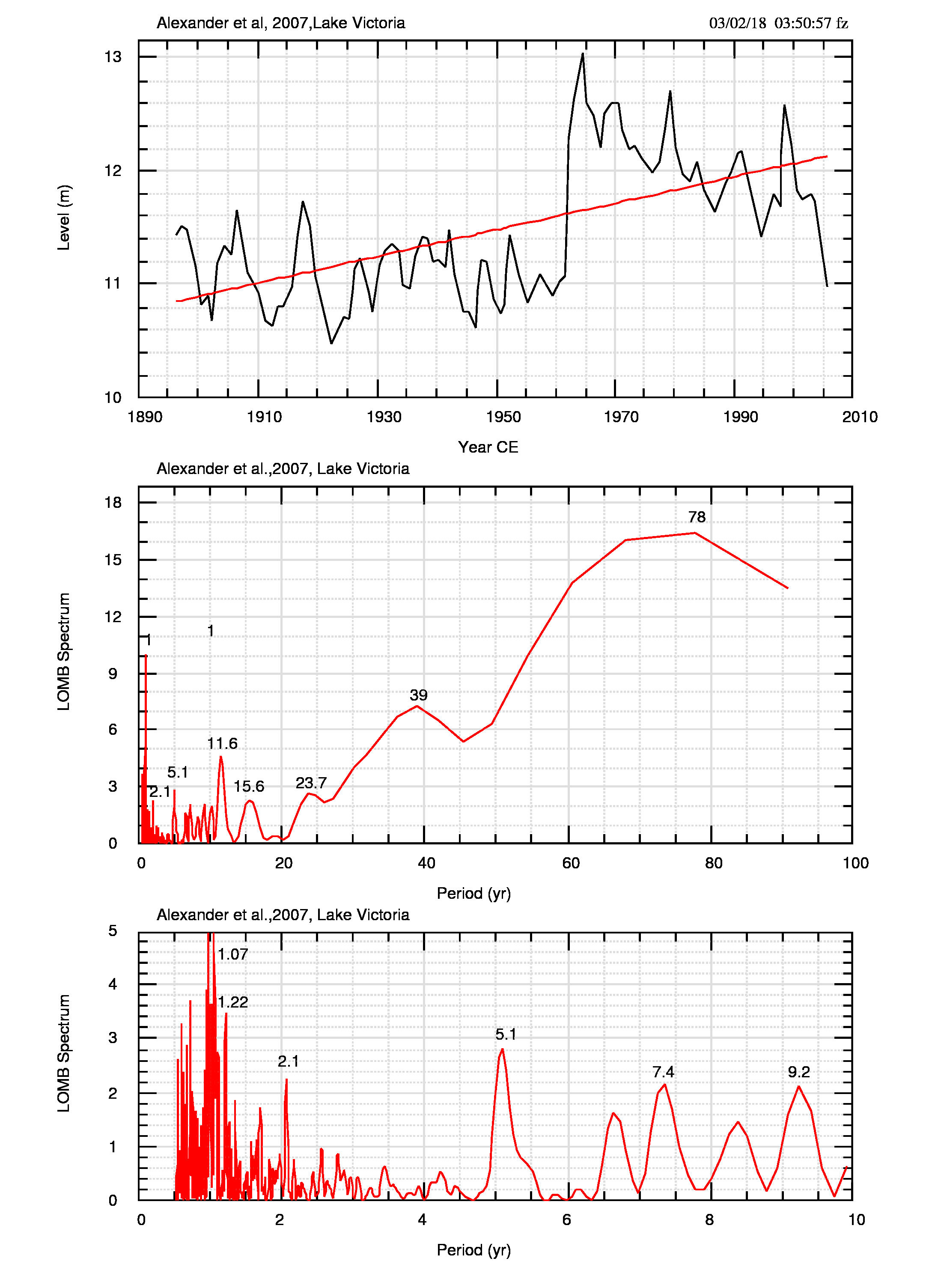
I massimi a 67-78 e 40 anni appaiono come macroscopiche caratteristiche spurie generate dalla persistenza, mentre quelli di periodo inferiore sono presenti anche negli spettri delle differenze/derivate.

Dati NOAA mensili
I dati e gli spettri mensili dei dati NOAA sono disponibili qui o meglio, nel momento attuale di difficoltà di accesso al server, qui.
Anche se si può immaginare una (forte) similitudine con i dati annuali, è bene fare una verifica anche sui dati mensili. Per questo controllo ho scelto i dati relativi a dicembre 2017 (1712t.dat) da cui ho calcolato le differenze (i dati sono a passo=1 mese, costante). Per entrambi i dataset ho calcolato la funzione di autocorrelazione, che mostro nella successiva figura 10 (pdf)

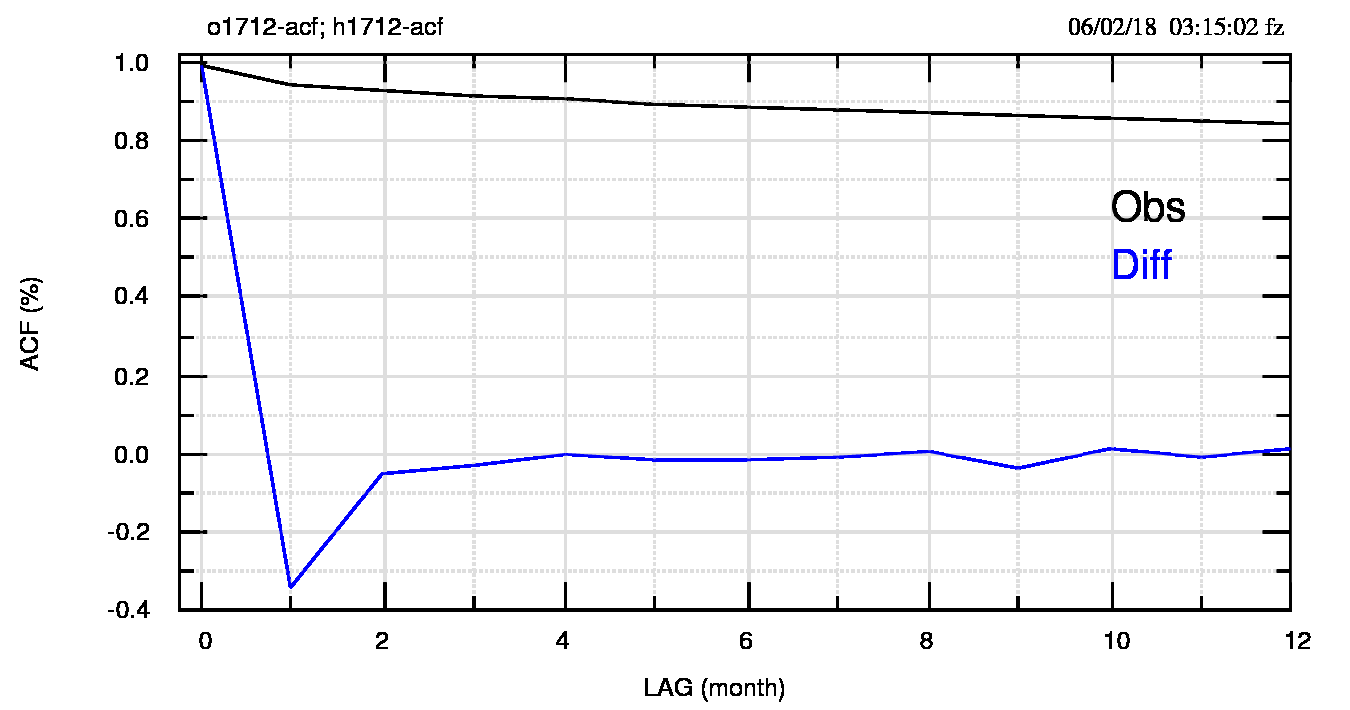
Qui si ripete, figura 11 (pdf) e figura 12 (pdf), il copione già visto per i dati annuali, accentuato in alcuni aspetti: usare le differenze permette di eliminare la persistenza (H_diff=0.5), mantenendo la stessa struttura spettrale ed aumentando il contrasto del massimo di circa 60 anni.

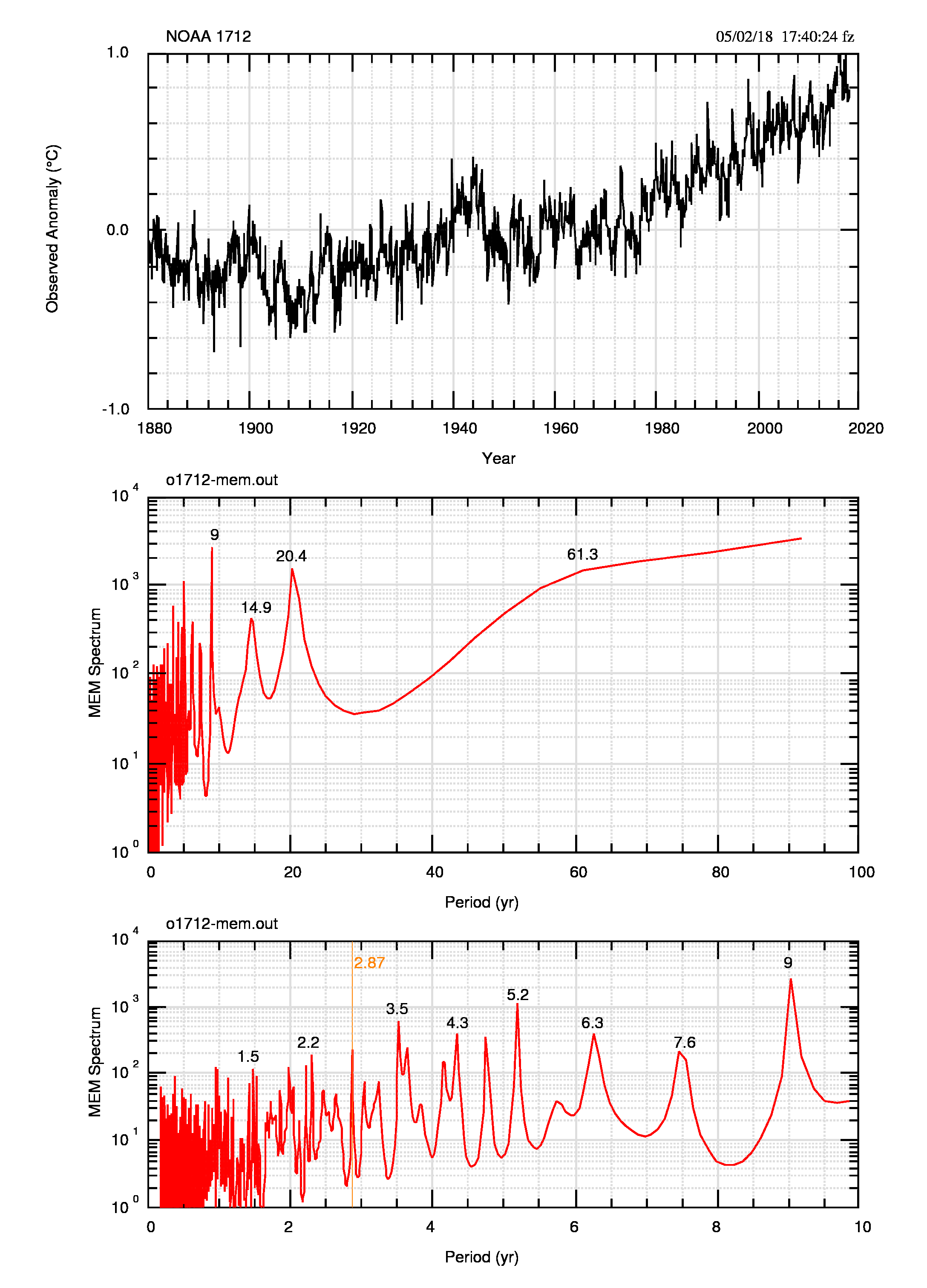
Cambia drasticamente la potenza che per i dati osservati è circa 100 volte quella delle differenze. Questo cambiamento dipende dal valore assoluto dei dati in ingresso ed è reso più evidente dal fatto che gli spettri non sono normalizzati (ad esempio alla potenza totale).

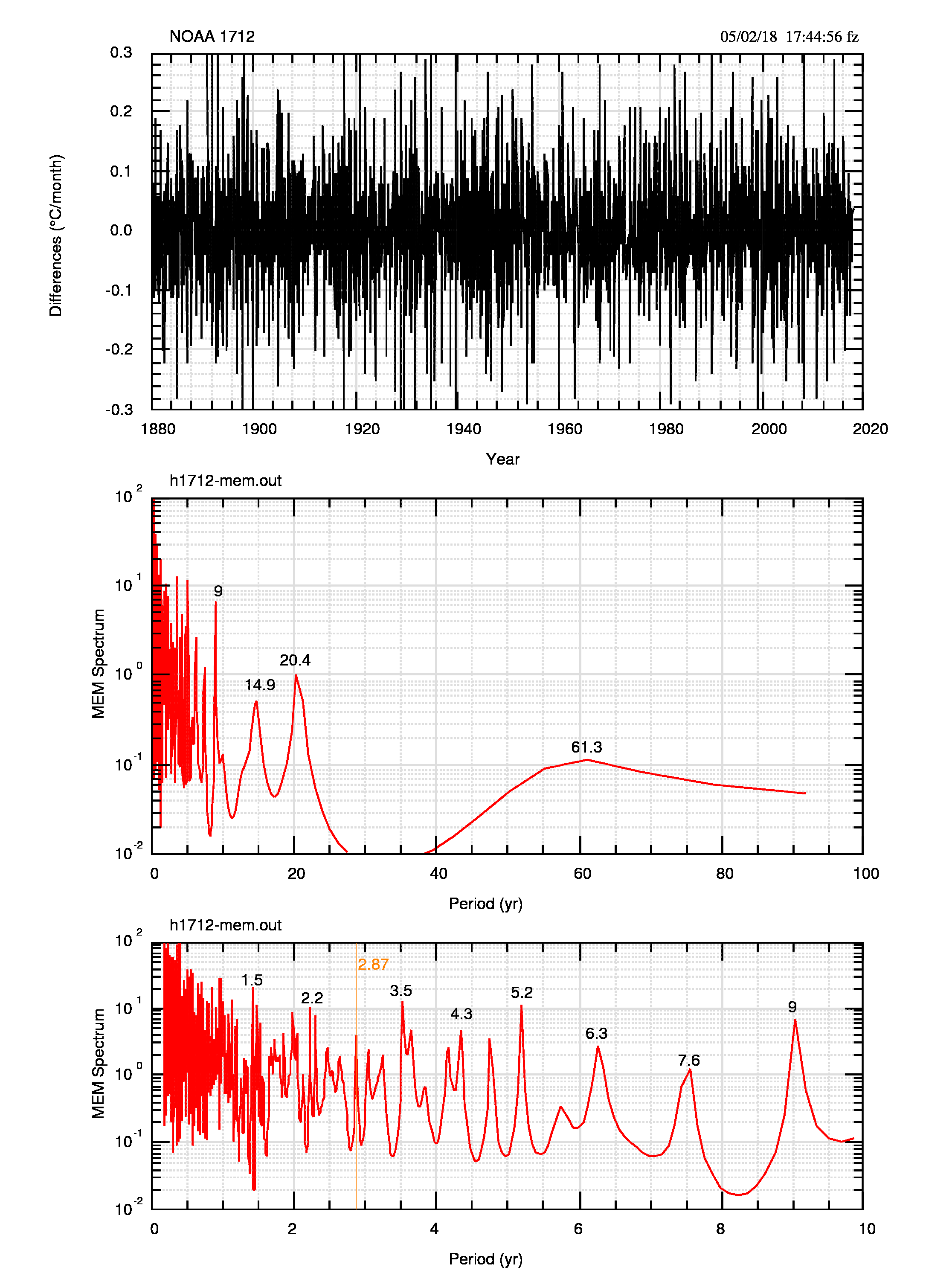
Dall’analisi dei dati mensili si evince l’uguaglianza spettrale con i dati annuali, oltre alla conferma che nel caso dei dati NOAA la persistenza, pur essendo molto forte, non incide significativamente sullo spettro. Solo nel caso del massimo di circa 60 anni l’uso delle differenze garantisce una migliore identificazione.
Le funzioni di autocorrelazione permettono di dire che le differenze riducono fortemente la persistenza (in pratica, la azzerano) anche in questo caso.

Considerazioni generali
Mentre le considerazioni appena espresse per i dati NOAA valgono anche per il caso generale, bisogna sottolineare che il miglioramento (riduzione) della persistenza non è della stessa entità in tutti casi.
Il livello del lago Vittoria mostra che le differenze e (in quel caso, con i dati non a passo costante) le derivate numeriche non tolgono del tutto la persistenza. Nello stesso tempo, però, mostrano un notevole miglioramento della struttura spettrale, con grande somiglianza tra gli spettri e differenze tra i periodi poco o per nulla significative. La modifica dei dati originali (differenze e derivate) permette di cancellare i massimi a circa 40 e circa 78 anni, la cui presenza era stata discussa, senza riuscire a capirne l’origine, qui su CM (anche nei commenti).
Da sottolineare ancora che, sebbene lo spettro dei dati osservati del lago Vittoria sia nettamente diverso dagli altri due (diff/deriv) per i periodi più lunghi, i periodi più brevi sono simili nei tre casi, suggerendo che forse la persistenza agisce in modo differenziato.

In conclusione, credo che l’uso delle differenze/derivate numeriche nelle serie con alto esponente di Hurst renda la loro analisi spettrale più certa, meno aleatoria, e nello stesso tempo sottolineo che è necessario verificare ogni volta la bontà della scelta di modificare i dati iniziali.

Bibliografia

1. Koutsoyiannis D.: The Hurst phenomenon and fractional Gaussian noise made easy, Hydrological Sciences-Journal-des Sciences Hydrologiques, 47:4, 573-595, 2002. doi:10.1080/02626660209492961
2. Koutsoyiannis D.: Climate change, the Hurst phenomenon, and hydrological statistics , Hydrological Sciences-Journal-des Sciences Hydrologiques, 48:1, 3-24, 2003. S.I. doi:10.1623/hysj.481.3.43481
3. Koutsoyiannis D.: Nonstationarity versus scaling in hydrology , Journal of Hydrology, 324, 239-254, 2006. doi:10.1016/j.jhydrol.2005.09.022