Tutti conosciamo le oscillazioni di marea che caratterizzano il livello marino e le cause che le determinano: l’attrazione gravitazionale del Sole e della Luna sulle masse idriche che costituiscono gli oceani ed i mari terrestri.
Le forze gravitazionali rappresentano le interazioni tra le masse, indipendentemente se esse sono liquide o solide, per cui anche le parti solide della Terra sono soggette alle stesse forze di marea, cui sono soggette le masse liquide. Le forze di marea che agiscono sulle masse solide terrestri, sono in grado di deformarle ed alterarne lo stato di moto? La risposta a questa domanda non è mai stata univoca, in quanto la viscosità del mantello è tale da rendere piuttosto difficile immaginare che le relativamente deboli forze di marea lunisolari, riescano a interagire in moto significativo con i moti delle placche tettoniche che costituiscono la crosta terrestre.
Ricordo a me stesso che la crosta terrestre è formata da placche tettoniche che “galleggiano” sul mantello sottostante. Il mantello risulta essere più denso e più fluido della crosta sovrastante e, inoltre, al suo interno si verificano dei moti convettivi che trasferiscono il calore del nucleo terrestre, verso la superficie della Terra. A questi flussi di calore sono associati, stante il tipo di trasmissione del calore, flussi di materia. Nel mantello si vengono a formare, quindi, immense celle convettive che fungono da “nastri trasportatori” per le placche tettoniche sovrastanti. L’intero sistema che ho sommariamente descritto, costituisce un sistema caotico auto organizzato.
La linea di pensiero principale sostiene che il movimento orizzontale delle placche è determinato esclusivamente dal meccanismo che ho appena finito di illustrare, ma qualcuno ha ipotizzato che le forze di marea lunisolari che determinano il rigonfiamento delle parti solide terrestri di alcune decine di centimetri, siano capaci di interagire con i movimenti orizzontali delle zolle tettoniche, modulandone il movimento, così come succede per le masse liquide che costituiscono gli oceani. La viscosità del mantello e le conseguenti forze di taglio che si generano lungo le superfici di separazione tra crosta e mantello e che si trasmettono anche agli strati superiori del mantello, sembra che inibiscano o rendano del tutto trascurabili gli effetti delle forze di marea lunisolari. Personalmente mi sono sempre riconosciuto in questo modo di pensare, per cui anni fa iniziai a seguire un poco la questione, ma dopo un po’ di tempo persi interesse per la cosa, proprio a causa di questi ragionamenti che, ripeto, condivido.
Da qualche giorno ho cominciato però ad avere qualche dubbio, in quanto ho avuto modo di leggere un interessante articolo pubblicato su Earth-Science Reviews
Tidal modulation of plate motions
a firma di D. Zaccagnino, F. Vespe e C. Doglioni (da ora Zaccagnino et al., 2020).
L’articolo è liberamente accessibile e, partendo dalle considerazioni che ho appena finito di esporre sinteticamente, dimostra che le forze di marea lunisolari sono in grado sia di modulare il moto delle placche tettoniche, sia di influenzare i terremoti di origine tettonica. Si tratta di ipotesi che innovano in modo determinante la dinamica delle masse terrestri, per cui le prove a sostegno dovrebbero essere piuttosto forti. La lettura dell’articolo, a parte alcune criticità che esporrò in seguito, mi ha convinto circa la solidità degli argomenti che gli autori portano a sostegno delle loro tesi.
Procediamo, però, in modo ordinato. La tettonica a zolle è nata in un periodo storico in cui era piuttosto difficile verificarne la validità scientifica: non era molto semplice misurare lo spostamento delle placche tettoniche, per cui la solidità della teoria è stata dimostrata in modo indiretto mediante studi che hanno interessato tutte le branche della geologia e della geodesia.
Con il progresso tecnologico che ha caratterizzato gli ultimi decenni, è stato possibile determinare con estrema precisione la posizione reciproca di punti particolari della superficie terrestre detti stazioni geodetiche. Le tecniche utilizzate per tali misurazioni sono di diverso tipo. Principalmente si utilizzano due flotte di satelliti: GNSS (che sta per Global Navigation Satellite System) e GPS (che sta per Global Position System) ed interferometri a grande base o VLBI (che sta per Very Large Baseline Interferometry). Una volta determinata la posizione reciproca di questi punti, si può procedere alla determinazione della lunghezza delle linee (baselines) che li uniscono e, quindi, determinare gli spostamenti reciproci tra gli stessi con precisioni dell’ordine del millimetro. La variazione di lunghezza di tali linee consente, mediante tecniche geodetiche, di determinare anche le rotazioni delle linee e, quindi, definire in modo completo la posizione nello spazio dei punti presi in considerazione. La variazione di posizione di tutti questi punti nel tempo, consente di determinare lo spostamento delle placche tettoniche sulla superficie terrestre, la loro reciproca rotazione, le variazioni dei dislivelli tra le stesse e le velocità relative con cui esse si allontanano o avvicinano.
Da quanto ho sin qui esposto, si capisce che le misurazioni di cui stiamo parlando, non costituiscono un dato chiaramente intellegibile, ma tale dato deve essere estratto da un segnale piuttosto rumoroso. Le variazioni di lunghezza delle baselines dipendono da diverse cause: variazioni climatiche (alternanza delle stagioni, del giorno e della notte, flussi di fluidi nel sottosuolo, pressione atmosferica), antropiche (generate dall’attività umana, come ad esempio modifiche delle strutture delle stazioni geodetiche) ed astronomiche (le forze mareali lunisolari). Alcune di queste cause determinano delle oscillazioni del segnale ad alta frequenza, altre a bassa frequenza. L’alternanza del giorno e della notte provoca, per esempio, oscillazioni ad alta frequenza della lunghezza di una baseline, come le variazioni della pressione atmosferica e delle temperature. Anche le forze di marea lunisolari determinano una vasta gamma di oscillazioni di cui alcune ad alta frequenza ed altre a bassa frequenza.
Se consideriamo le oscillazioni di marea diurne che caratterizzano gli oceani, avremo le corrispettive oscillazioni anche nelle lunghezze delle linee che hanno gli estremi nelle stazioni geodetiche, ma le forze di marea lunisolari che agiscono sulle masse terrestri, non sono solo quelle circadiane o mensili, ma sono caratterizzate da frequenze diverse. Cerchiamo di capire quali sono queste frequenze diverse da quelle diurne e mensili.
Le posizioni del Sole e della Luna che determinano le maree sulla Terra, cambiano, infatti, non solo nell’arco delle ventiquattro ore o mensilmente o annualmente, ma anche secondo cicli pluriennali. Nelle scorse settimane Franco Zavatti ci ha illustrato come le piogge ed altri eventi atmosferici, presentino andamenti che consentono di individuare periodi di 18,6 anni o di 8,85 anni circa, oltre alle armoniche superiori ed inferiori. Quando ho letto i lanci di agenzia con cui si segnalava l’articolo di Zaccagnino et al., 2020, pertanto, mi sono subito incuriosito ed ho deciso di approfondire la questione. Zaccagnino et al., 2020 ha poco a che fare con il clima e con gli argomenti di cui discutiamo su queste pagine. Ho deciso, però, di scrivere questo articolo, perché Zaccagnino et al., 2020, mette in evidenza come le influenze astronomiche siano in grado di modulare fenomeni terresti tra i più vari. Negli anni scorsi ho avuto la fortuna di leggere e commentare diversi articoli di Nicola Scafetta, in cui si individuavano relazioni tra i fenomeni climatici ed i cicli astronomici di diversi pianeti. Zaccagnino et. al., 2020 mi ha consentito di completare il quadro, in quanto permette di comprendere quanto sia stretto il legame tra il nostro pianeta ed i suoi “vicini” astrali (in questo caso Sole e Luna).
Prima di proseguire, un piccolo accenno al tipo di fenomeni astronomici di cui ci occuperemo: i cicli lunari di 18,6 anni e di 8,85 anni. Questi due periodi sono caratteristici dei complessi moti del sistema dinamico Terra-Luna, sollecitato dalle forze gravitazionali solari. Il periodo di 18,6 anni o periodo della precessione nodale, rappresenta il tempo impiegato dalla retta passante per i nodi ascendente e discendente, a compiere una rotazione completa. Il periodo di 8,85 anni o periodo della precessione degli apsidi, rappresenta il tempo impiegato dalla linea degli apsidi a compiere un giro completo.
Zaccagnino et al., 2020 si pone l’obiettivo di individuare se tra le oscillazioni che caratterizzano le lunghezze delle baselines, compaiono anche in questi due periodi, ovvero quello della precessione nodale e quello della precessione della linea degli apsidi. Nell’articolo vengono citate tutta una serie di situazioni che fanno intuire che il movimento delle placche possa essere guidato da qualcosa che si sovrappone al nastro trasportatore convettivo caotico auto organizzato. Tra tutte le circostanze prese in considerazione da Zaccagnino e colleghi, quella che mi ha maggiormente incuriosito, è un’asimmetria negli spostamenti delle placche che sembra distinguere tra oriente ed occidente. Si nota, infatti, una leggerissima prevalenza degli spostamenti e delle rotazioni delle placche diretto verso ovest. In un processo caotico seppur auto organizzato, questo stona parecchio.
Partendo da queste considerazioni, Zaccagnino et al., 2020, formulano la seguente ipotesi: se le distanze tra due stazioni geodetiche sono modulate dalle distanze relative Sole-Luna-Terra, esse devono oscillare con frequenze che siano inverse del periodo di precessione nodale e del periodo di precessione degli apsidi, ovvero 18,6 anni ed 8,85 anni.
Prima di procedere oltre, reputo necessario un sintetico riferimento storico. Le oscillazioni di marea costituiscono un rompicapo fin dalla più lontana antichità. Che le maree seguano dei periodi ben precisi è noto, ma il problema è prevederle in modo esatto. E’ stato facile, per me, dire che le variazioni delle distanze reciproche Terra-Luna-Sole sono in grado di determinare variazioni della distanza tra le stazioni geodetiche, ma tra l’aspetto qualitativo e quello quantitativo, ce ne passa. Molti si sono cimentati nel tentativo di prevedere le maree con metodi analitici. Chi diede un contributo fondamentale all’impresa, fu Laplace che scrisse una serie di equazioni alle derivate parziali che descrivevano il comportamento di una lamina liquida, soggetta alle forze gravitazionali di Terra, Luna e Sole: si tratta di equazioni fluidodinamiche. Il metodo fu perfezionato da Lord Kelvin che applicò l’analisi armonica di Fourier al moto delle maree e da G. Darwin (figlio di Charles). Fu nel 1921, però, che la previsione analitica delle maree cominciò ad essere applicata in modo efficace, grazie al contributo di A. T. Doodson che introdusse una serie di numeri (Doodson numbers) in grado di ricostruire lo spettro di 388 frequenze che caratterizzano l’analisi armonica del moto delle maree. Si tratta di numeri, determinati empiricamente e che inseriti nelle equazioni, consentono di ricostruire in modo praticamente perfetto le oscillazioni di marea.
Dopo questa parentesi storica, torniamo a Zaccagnino et al., 2020. Gli autori hanno applicato una particolare analisi di Fourier (Fast Fourier Transform o FFT) ai dati (misura delle baselines) e dei particolari numeri di Doodson per creare un modello di oscillazioni di marea, da confrontare con il segnale della velocità relativa con cui variano le distanze tra dieci coppie di stazioni geodetiche che coprono quasi tutto il globo terrestre. I dati sono stati sottoposti ad un primo filtraggio mediante un algoritmo statistico (media mobile a trenta giorni) per eliminare le oscillazioni ad altissima frequenza e, successivamente, si sono estratte le frequenze dal segnale così ottenuto, mediante la trasformata di Fourier veloce. Eliminata la tendenza lineare che caratterizzava il segnale, i ricercatori hanno confrontato i residui così ottenuti e, quindi, i dati, con le oscillazioni di marea lunisolari ottenute considerando sette armoniche (periodi di 4 mesi, 6 mesi, un anno, 3,57 anni, 8,85 anni, 9,3 anni e 18,6 anni) ed i relativi numeri di Doodson.
In tutti e dieci i casi presi in considerazione, le curve sperimentali e quelle teoriche sono caratterizzate da una correlazione molto elevata (intervallo di confidenza nell’ordine del 95%, ovvero 2σ), per cui i ricercatori giungono alla conclusione che le variazioni delle distanze relative tra le varie stazioni geodetiche prese in considerazione, sono in fase con il ciclo dei nodi lunari e quello degli apsidi e, pertanto, questi cicli astronomici “modulano” le variazioni della velocità con cui si spostano le placche tettoniche. A titolo puramente esemplificativo, riporto una figura tratta dalla fig. 9 di Zaccagnino et al., 2020.
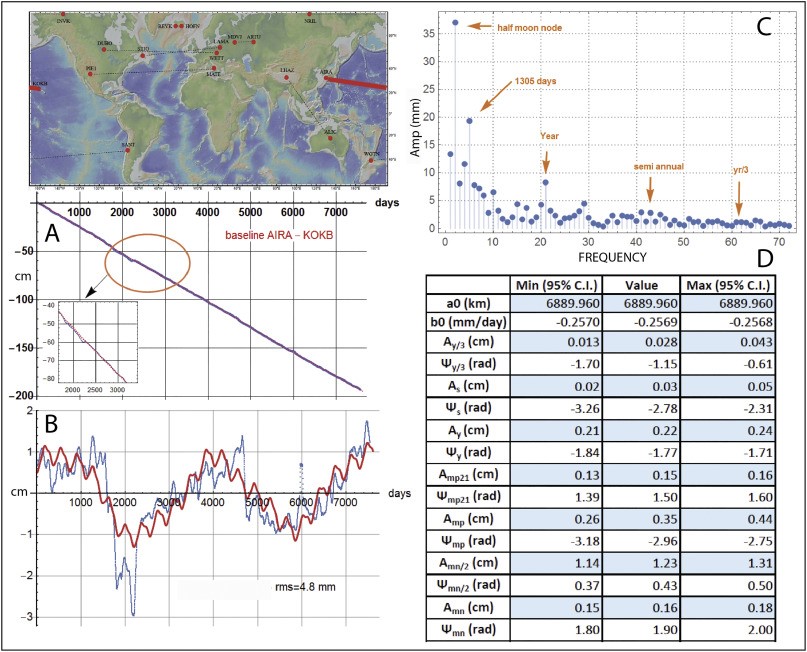
Poiché correlazione non è causalità, è opportuno cercare di capire il meccanismo fisico con cui la Luna ed il Sole sono in grado di interagire con la tettonica planetaria. Per comprendere il meccanismo fisico con cui le forze di marea influenzano lo spostamento delle placche, è necessario accennare brevemente a cosa succede lungo la linea di contatto tra litosfera e mantello. Il mantello è roccia, ma queste rocce si trovano ad una temperatura molto elevata, per cui hanno un comportamento viscoso. La viscosità del mantello non è, però, uniforme, ma varia radialmente. Si distinguono, pertanto, diverse zone che hanno viscosità differenti. Ai fini del nostro discorso ci interessa quella che i geologi definiscono Low Velocity Zone (LVZ) o anche zona di disaccoppiamento. Si tratta di una zona relativamente fluida che rallenta molto le onde sismiche, da cui il nome. Zaccagnino et al., 2020 è dell’avviso che questa zona funge da “filtro passa basso” per le forze di marea. Seguendo il loro ragionamento, che qui non riporto per motivi di sintesi, le oscillazioni di marea a frequenza più alta vengono “ammortizzate” dalla viscosità del mantello superiore e della litosfera, mentre quelle a frequenza più bassa non vengono attenuate dalla viscosità del mantello e, grazie alla zona di disaccoppiamento, riescono ad interagire efficacemente con il movimento delle placche tettoniche.
Una parte dell’articolo di Zaccagnino et al., 2020 è dedicata anche ai terremoti: secondo gli autori le componenti orizzontali delle forze di marea, alterando la velocità di spostamento reciproco delle placche, sono in grado di modulare l’attività sismica tettonica in modo più efficace delle componenti verticali di tali forze. Preferisco soprassedere dal descrivere le complesse interazioni tra forze di marea, tensioni normali e tensioni tangenziali che caratterizzano gli stati tensionali delle strutture rocciose che costituiscono litosfera ed astenosfera e che giustificano le conclusioni di Zaccagnino et al., 2020, rinviando i lettori interessati all’articolo originale.
Ho cercato di sintetizzare al massimo e nel miglior modo possibile l’articolo di Zaccagnino e colleghi e, probabilmente, ho semplificato eccessivamente alcuni concetti che avrebbero avuto necessità di maggior spazio e dettaglio, ma per i fini che mi prefiggo, credo che il livello di dettaglio sia sufficiente.
In linea di massima Zaccagnino et al., 2020 mi convince, anche se restano diverse perplessità delle quali riporto quelle, secondo me, più rilevanti.
La prima riguarda la lunghezza delle serie di dati. Gli autori sostengono di aver preso in considerazione quelle più lunghe, ma esse hanno tutte durata inferiore ai 30 anni. La trasformazione di Fourier opera in modo affidabile per lunghezze delle serie doppie dei periodi che si prendono in considerazione: nessuna delle serie considerate ha lunghezza maggiore o uguale al doppio del periodo di 18,6 anni, per cui gli autori hanno dovuto far ricorso a delle estrapolazioni basate sul principio dei minimi quadrati che mi lasciano un po’ freddo. La metodologia utilizzata, però, mi sembra affidabile, per cui quando avremo a che fare con serie più lunghe, probabilmente le conclusioni dell’articolo potranno essere confermate.
Altra perplessità riguarda il meccanismo fisico con cui le forze di marea lunisolari interagiscono con la litosfera e l’astenosfera. Gli autori fanno riferimento al tempo di Maxwell, ovvero al tempo che impiega un materiale a reagire alle azioni cui viene sottoposto e che dipende dalla viscosità dei materiali. Secondo gli autori il tempo di Maxwell della litosfera e della parte di mantello posta al di sopra della zona di disaccoppiamento, è maggiore del periodo delle oscillazioni ad alta frequenza delle maree lunisolari e, quindi, impedisce che queste abbiano effetti sulle dinamiche crostali. Il tempo di Maxwell della zona a bassa velocità, invece, è compatibile con le oscillazioni a bassa frequenza. Personalmente reputo che questi calcoli siano affetti da elevata incertezza.
Concludendo, mi sento di affermare che se le forze di marea lunisolari sono in grado di modulare spostamenti come quelli delle placche tettoniche, a maggior ragione potrebbero essere in grado di modulare le dinamiche oceaniche ed atmosferiche e, quindi, i fenomeni climatici analizzati da F. Zavatti nelle scorse settimane.


In questo post il signor Donato Barone ricorda che
– la crosta terrestre è formata da placche tettoniche che “galleggiano” sul mantello sottostante. Il mantello risulta essere più denso e più fluido della crosta sovrastante e, inoltre, al suo interno si verificano dei moti convettivi che trasferiscono il calore del nucleo terrestre, verso la superficie della Terra. A questi flussi di calore sono associati, stante il tipo di trasmissione del calore, flussi di materia. Nel mantello si vengono a formare, quindi, immense celle convettive che fungono da “nastri trasportatori” per le placche tettoniche sovrastanti. L’intero sistema che ho sommariamente descritto, costituisce un sistema caotico auto organizzato. –
Quindi passa ad illustrare gli effetti delle maree lunisolari sulle placche, se sia possibile prevederle e come, alla luce delle nuove misurazioni rese possibili dalla nuove tecnologie satellitari sul calcolo delle posizioni sulla superficie terrestre.
Tutto ciò è basato sulle possibili influenze che luna e sole, possono esercitare con la loro attrazione, causando tipi di maree con diverse frequenze e cicli.
Vorrei sottoporre alla sua attenzione, ma anche a quella di chiunque, l’ipotesi che possano esistere effetti che di manifestino, o che per lo meno esercitino la loro influenza, anche intervenendo dall’interno della Terra.
Dopo tante ere geologiche si è ormai cristallizzata, definita, una mappa di tutti i movimenti convettivi che animano la dinamica del mantello sottostante la crosta terrestre. L’innalzamento di molte catene montuose è in atto da millenni, e ciò ostacola sempre più la circolazione delle correnti atmosferiche, lo scambio di calore fra nord e sud, rendendolo meno graduale e progressivo. Si pensi che approssimativamente un terzo della massa di acqua ed aria, ad ogni cambio di stagione, supera l’equatore, passando da un emisfero all’altro, da nord a sud, due volte l’anno. Questo spostamento di peso, trascurato forse per la sua relativa “piccola entità”, non incide solo direttamente sulla crosta terrestre, ma varia la posizione del baricentro del pianeta. Il nucleo più pesante ed interno del pianeta, per sei mesi all’anno è spinto verso nord e per i restanti mesi verso sud, dato che tende a posizionarsi versi il baricentro gravitazionale della Terra e non tende a rimanere immobile presso il suo centro geometrico. C’è quindi uno stantuffo al centro della Terra che fa “su e giù” due volte l’anno, forse per pochi metri. Analizzando le statistiche, nel mio piccolo, ho notato che tra i terremoti di maggiore potenza, alcuni si verificano lo stesso giorno dell’anno anche tre volte di seguito, sia pure in luoghi diversi del pianeta. Non esistono solo aree sismiche quindi, zone dove i terremoti e le eruzioni son più probabili, ma anche stagioni, periodi, tempi sismici. A riprova che lo spazio ed il tempo sono intimamente connessi, chi è in possesso di dati completi potrebbe meglio sostenere ed illustrare che non esistono solo zone, ma anche tempi sismici.
Ora io non sono uno specialista, posso chiedere se questo aspetto è stato già trattato?
Grazie
Moreno Fontanas
Le sue osservazioni mi sembrano molto interessanti. Leggendo l’articolo di Zaccagnino e colleghi ho visto che essi hanno inserito tra le cause delle oscillazioni ad alta frequenza anche quelle climatiche. Tra le cause climatiche essi hanno parlato di temperature e stagioni. Diciamo che potrebbero essere collegate alle sue osservazioni. Devo approfondire la questione con i lavori cui gli autori fanno riferimento, ma in questo momento non ho molto tempo. Spero di poterlo fare a breve.
.
Nella fase di analisi del fenomeno, però, essi hanno eliminato le oscillazioni ad alta frequenza in quanto interessati solo alle oscillazioni a bassa frequenza (poliennali).
Ciao, Donato.
Prof. Barone, mi fa fare le ore piccole pubblicando articoli così interessanti!
Grazie di cuore, Alvaro
P.S. aiuta anche a capire come i terremoti siano spiacevoli, ma necessari – senza di loro non ci sarebbero terre emerse e la specie umana si troverebbe come nel film “Waterworld” 🙂
Troppo buono. Sono molto contento, però, di averla interessata.
Ciao, Donato.
Caro Donato,
questa volta ti sei cimentato, con la ormai abituale chiarezza, con un problema che ai miei occhi appare molto complicato. L’analisi dei dati VLBI è qualcosa che esula dalla mia competenza e richiede controlli molto accurati sull’istante delle osservazioni e sulla sincronizzazione dei ricevitori da una parte all’altra del mondo. A Bologna abbiamo una delle stazioni VLBI e i nostri radioastronomi usano quell’antenna dall’inizo per immagini radio ad alta risoluzione (millesimo di secondo d’arco) di oggetti celesti molto distanti. Ho quindi sentito molto parlare della tecnica ma non ne conosco i dettagli, che in geodesia sono diversi rispetto a quelli della radio astronomia.
Quindi non posso fare altro che prendere i risultati degli autori senza essere in grado di commentarli: noto però che gli autori usano sia il massimo spettrale di 18.6 anni che le sue armoniche (e quelle di altri massimi). Questo fatto “mi torna” meglio di quello usato per El Nino in cui sono presenti solo le armoniche e non il picco principale. Se poi il VLBI
riesca ad evidenziare oscillazioni di così alta frequenza nel moto delle placche non saprei, e a me sembrano oscure le loro figure C che non riesco a capire. Mi sarebbe piaciuto che avessero pubblicato (o reso disponibili) i dati delle figure B (blu) per poter rifare gli spettri e capire meglio. Forse chiederò i dati agli autori.
Intanto, nel dicembre 2017, in http://www.climatemonitor.it/?p=46742 ho parlato del picco di 18.6 anni in vari dati connessi con il Canale
Faroe-Shetland e in uno scambio di commenti con Gianni (sempre lui, benemerito!) avevo scritto che non avevo trovato quel picco nello spettro delle coordinate x,y della posizione del Polo. In realtà il massimo è a
18.3 anni, del tutto compatibile con 18.6 ma allora non ero abbastanza sensibilizzato al problema (accludo in fondo lo spettro del moto del Polo). Posso pensare che il moto del Polo risenta dello spostamento delle placche e questo fatto rafforza l’idea che gli autori abbiano ragione, a prescindere dalle mie ignoranze geodetiche.
Per concludere due punti minori: gli autori usano la terminologia “C.I. del 95% ovvero 2 sigma”: basta prendere una tavola della distribuzione normale per vedere che il 95% corrisponde a 1.96 sigma (un numero molto noto in statistica). E’ vero che 2 (95.44%) è una buona approssimazione di 1.96 ma
quella affermazione mi è suonata come un dito (leggermente) piantato in un occhio.
Secondo punto: gli autori ringraziano, tra gli altri, Dino Boccaletti che è stato nel 1969 il mio docente di Istituzioni di Fisica Teorica, tuttora indimenticato e ammirato. Gli auguro ogni bene. Franco
Immagine allegata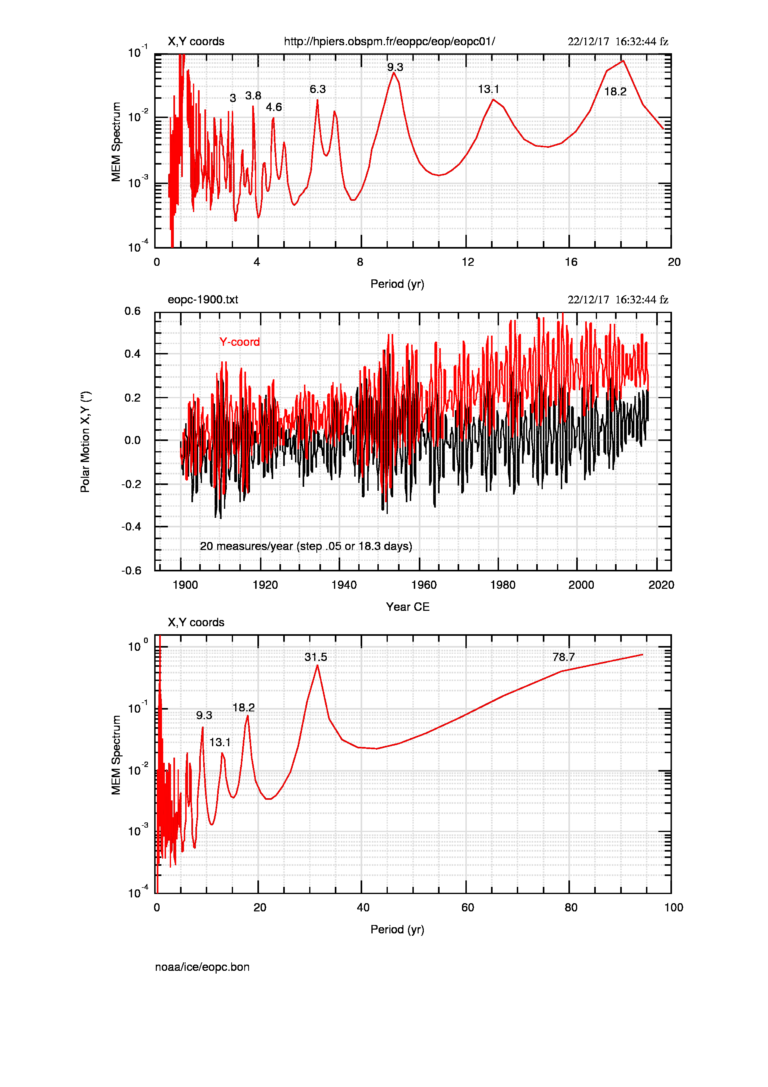
Caro Franco,
la principale fonte di dati dello studio è costituita dagli archivi GNNS integrati con i dati GPS: le stazioni geodetiche sono geolocalizzate mediante trigonometria solida con vertici nei satelliti delle costellazioni GNNS e GPS e nelle stazioni geodetiche. Le basi VLBI vengono utilizzate come vertici geodetici riferiti ad un sistema inerziale celeste costituito da diverse centinaia di QUASAR: data la loro grande distanza, esse costituiscono un sistema di riferimento quasi-inerziale. Le antenne radio dei vertici di una baseline VLBI captano il fronte d’onda proveniente dalle QUASAR che, data la grande distanza, può essere considerato piano. Lo sfasamento con cui esso viene ricevuto dalle stazioni poste agli estremi della baseline, consente di determinare la lunghezza della stessa e, quindi, le sue variazioni.
.
Nell’antichità si utilizzavano tecniche basate sulla parallasse per individuare le distanze dei pianeti e dei satelliti dalla Terra, ma tale tecnica era inefficace per le stelle. Oggi si utilizza una tecnica simile per misurare la lunghezza della linea alle cui estremità sono posti due ricevitori.
.
Circa la tabella C di Zaccagnino e colleghi, in base a quello che mi è parso di capire, dovrebbe rappresentare le oscillazioni delle lunghezze delle baselines in funzione delle varie frequenze della trasformata di Fourier veloce. Mi sembra una specie di spettro di potenza delle varie frequenze, in cui la potenza è rappresentata dalle ampiezze delle oscillazioni della lunghezza della baseline.
.
Per quel che riguarda l’intervallo di confidenza non posso che essere d’accordo con te.
Allo stesso modo concordo con te circa le problematiche della posizione dei poli magnetici e la presenza del periodo di precessione nodale lunare, nei dati da te esaminati: potrebbe essere un’ulteriore conferma delle influenze celesti nei fenomeni terrestri.
.
E per finire un grazie sentito per il tuo importante contributo alla comprensione di questo articolo di cui la geodesia rappresenta solo una parte (quella che mi è più congeniale), mentre la restante parte non è di facile, né agevole comprensione.
Se tu dovessi essere in grado di avere i dati dagli autori, ne sarò estremamente felice in quanto potremmo vedere le cose da una diversa prospettiva.
Ciao, Donato.
Scusate ma mi sorge un grosso dubbio. L’effetto di fenomeni di questo tipo dovrebbe essere soggetto all’inerzia del sistema , invece sembra perfettamente sincronizzato coi cicli lunari .Capisco che l’inerzia dell’ atmosfera potrebbe essere bassa ma quello delle masse tettoniche è enormemente più grande di quello atmosferico . Come fanno ad essere sincronizzati ?
come al solito… correlazioni.
Non causa-effetto.
La scienza delle correlazioni è: opinione.
“L’effetto di fenomeni di questo tipo dovrebbe essere soggetto all’inerzia del sistema, ….”
.
Lo è. Nell’articolo e nel mio commento si parla di effetti delle oscillazioni ad alta frequenza che sono ammortizzati dalla viscosità della litosfera e della parte superiore del mantello. Per un non geologo come me, c’è voluto del tempo per capire la questione che è complessa. Secondo gli autori la reologia delle rocce del mantello e della crosta è tale da impedire che le forze di marea con ciclo diurno, mensile ed anche di un terzo di anno abbiano effetto sulla lunghezza delle baselines.
.
Il tempo di Maxwell della crosta e della parte di mantello immediatamente sottostante, fino alla zona di disaccoppiamento, è tale da impedire a queste azioni di produrre effetti consistenti. Diciamo che a questi periodi non si riscontrano effetti apprezzabili, per cui il sistema ha un elevato grado di inerzia. Se consideriamo, però, la zona di disaccoppiamento, si nota che la viscosità diventa molto più bassa ed il tempo di Maxwell diminuisce notevolmente. Per azioni orizzontali esso si riduce a pochi decenni, per cui la componente orizzontale delle forze di marea con periodi dell’ordine del decennio (periodo degli apsidi e periodo nodale) sono in fase con i tempi di rilassamento della zona di disaccoppiamento che si comporta quasi come un corpo elastico.
.
Sono perfettamente cosciente che questo diverso comportamento del mantello, questa spiccata anisotropia dell’astenosfera, rappresenti una criticità molto evidente del modello considerato da Zaccagnino e colleghi, ma su questo si può lavorare.
Ciao, Donato.