Le anomalie di temperatura rese disponibili dal NOAA e scaricabili da qui sono state aggiornate con i dati relativi al mese di Gennaio 2012.
Come è noto, questo file mantiene sempre lo stesso nome anche se ogni mese viene ricalcolato con algoritmi che coinvolgono tutti i dati, a partire dal 1880; ogni mese i dati mensili medi delle anomalie di temperatura vengono modificati di quantità dell’ordine di qualche millesimo di grado centigrado. Mi sono proposto di verificare di quanto cambia il file ogni mese e avevo iniziato il confronto tra i dati fino a novembre 2011 e quelli fino a dicembre 2011 su Climate Monitor qui e anche qui (per favore prendere nota: per un motivo che non conosco, se si tenta di accedere al mio server con www.zafzaf.it si ottiene l’errore “not found”. Bisogna accedere con zafzaf.it – quindi senza il www- e va tutto bene).
Adesso che c’è il nuovo aggiornamento, ho fatto il confronto tra novembre e gennaio e ho cercato di capire il senso dei valori negativi e positivi delle differenze di anomalie.
Le anomalie sono calcolate come differenza tra la temperatura mensile media mondiale e una temperatura di riferimento Tr. Quando scriverò TNov intenderò le temperature fino a novembre 2011 e quindi farò riferimento al file che contiene le anomalie fino a novembre 2011, e la stessa cosa varrà per gli altri mesi: anomalieNov=TNov-Tr; anomalieDic=TDic-Tr, ecc …
Se Tr è costante, cioè se Tr non viene calcolata ogni volta usando il file delle temperature ricostruito dopo l’aggiunta di un nuovo mese, si ha:
Δ= anomalieNov – anomalieDic= TNov-Tr – TDic+Tr = TNov-TDic
e i grafici delle differenze di anomalie rappresentano le differenze di temperatura tra due file NOAA scelti per il confronto.
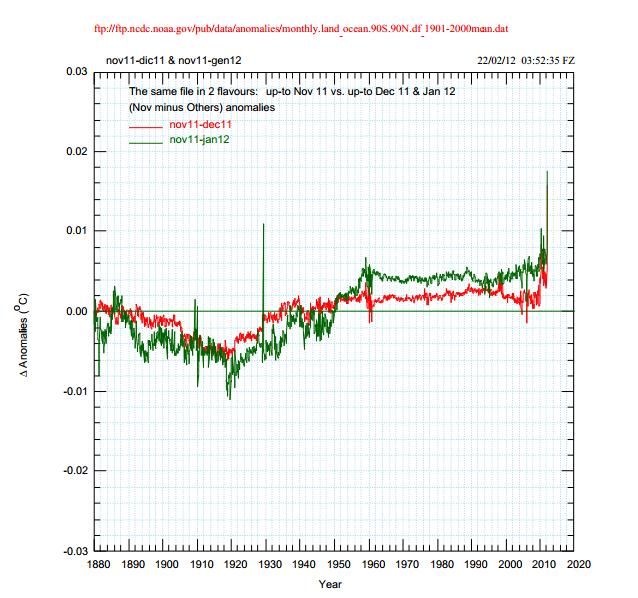
Dal grafico in cui sono mostrate le differenze di temperatura TNov-TDic (in colore rosso) e TNov-TGen (in colore verde) si deduce che:
- nelle zone in cui il grafico è negativo (dal 1890 al 1935 o al 1950 circa) TNov-TDic < 0, cioè TNov<TDic e il”file vecchio” è “più freddo” del file “nuovo” oppure, viceversa, i nuovi dati sono più caldi dei vecchi.
- al contrario, quando il grafico è positivo (dal 1935 o dal 1950 al 2012), TNov>TDic e il file “vecchio” è “più caldo” del file “nuovo”, ovvero i nuovi dati sono più freddi dei vecchi.
- le stesse considerazioni si applicano anche a TNov-TGen (intendendo gennaio 2012) con in più:
- le differenze di temperatura rispetto a novembre raddoppiano (o quasi) per gennaio in confronto a dicembre. Se le variazioni continueranno nello stesso verso e con lo stesso ritmo, sarà facile raggiungere i centesimi e poi i decimi di grado.
- l’anno in cui le differenze sono nulle si sposta da circa il 1935 a circa il 1950.
Non bisognerebbe dimenticare che i tre file usati in questa nota sono formalmente lo stesso file. Tutti i dati presentati mostrano differenze di alcuni millesimi di grado rispetto allo zero (a parte 2 o 3 picchi poco significativi), ben più piccole delle incertezze di misura e di elaborazione dei dati di temperatura. Le variazioni presentate potrebbero (e in teoria dovrebbero) “lasciare il tempo che trovano” ed essere considerate fluttuazioni statistiche se non fosse per gli andamenti sistematici (e, almeno per ora, di ampiezza crescente) che fanno sospettare un algoritmo di filtraggio e di ricostruzione dei dati in grado di produrre effetti ben visibili -che per di più diminuiscono1 il gradiente di temperatura degli ultimi 132 anni- quando si aggiunge un dato ai 1583 precedenti (lo 0,06%).
Nei prossimi mesi continuerò a salvare il file più recente e a confrontare i nuovi dati con quelli di novembre 2011.
Addendum
Mi permetto un’incursione nel post di Franco per segnalarvi questo post su Tallbloke’s Talkshop, dove viene messo in evidenza lo stesso problema per i dati delle boe oceanografiche del sistema ARGO. Dati preziosi sebbene piuttosto giovani – il dispiegamento delle boe è iniziato nel 2003 ed attualmente ne sono state posate circa 3600 – il cui utilizzo è però coinciso con una fase di relativa stabilità sia delle SST (temperature di superficie), sia dell’OHC (contenuto di calo0re degli oceani). Anzi, le prime analisi di questi dati, ad esempio per il periodo 2003-2007, mettevano in evidenza un debole trend negativo. Successivamente, per effetto di alcune correzioni resesi evidentemente necessarie, il trend è diventato debolmente positivo.
Boh…
gg
- dai grafici potrebbe sembrare che il gradiente aumenti ma in realtà aumenta la variazione nelle differenze di temperatura. Questo si traduce in “nuove temperature maggiori nel periodo pre-1935 (o pre-1950) e minori nel periodo post-1935 (o post-1950)” e quindi in un appiattimento delle temperature e conseguente diminuzione del gradiente. [↩]


Franco,
ho dato uno sguardo alle fonti che hai citato (grazie per la segnalazione) e, onestamente, il mistero si infittisce. Per ammissione degli stessi curatori del dataset, infatti, le anomalie vengono calcolate rispetto ad una media di riferimento che copre tutto il 20° secolo (dal 1901 al 2000) per cui il ragionamento che tu hai sviluppato è perfettamente logico e coerente con l’impostazione del dataset. Dobbiamo augurarci che la brusca variazione delle anomalie fatta registrare da gennaio 2012 su novembre 2011 rispetto a quella di dicembre 2011 su novembre 2011, sia da imputare al nuovo dataset introdotto dalla NOAA. Il nuovo set di dati, comunque, ha modificato tutte le anomalie della serie storica a partire dal 1880. Questo significa che i dati per il calcolo della Tr relativa al periodo 1901/2000 hanno subito notevoli variazioni. Se non ho equivocato nel tradurre i contenuti della pagina NOAA, sembra che siano stati eliminati dei dati satellitari in quanto soggetti ad un non meglio identificato bias. Fosse questa la spiegazione? Come giustamente fai notare è opportuno aspettare ancora qualche giorno e vedere che succederà con i nuovi dati. Infine una piccola nota di colore. Quando ho fatto riferimento all’algoritmo di ricostruzione dei dati effettivamente pensavo ad un algoritmo di “massaggio” (nel senso di Mann) dei dati 🙂 . Mi fa piacere sapere che quello a cui facevi riferimento è un altro tipo di algoritmo.
Se è così non ho nulla da obiettare, anzi mi scuso per la malizia del mio precedente commento.
Ciao, Donato.
Donato,
grazie per i commenti, come al solito puntuali e precisi.
Anche io avevo individuato il problema nella (mancanza di) costanza di Tr, evidenziato anche dallo spostamento dell’anno in cui si passa da differenze positive a differenze negative. E per questo avevo sottolineato che tutto il mio ragionamento aveva senso solo se Tr fosse stata costante.
Nella pagina NOAA (NCDC), se cerchi il paragrafo “Global Mean Monthly Surface Temperature…” , il secondo nell’elenco di fianco alla figura di inizio pagina, potrai verificare che la temperatura media terra-mare 1901-2000 (direi proprio quella che io ho chiamato Tr) sembra essere quella (una media di 13.9 °C) e basta, senza ricalcolarla ogni volta.
Nella stessa pagina NOAA, però, viene messo in evidenza il fatto che le temperature sono cambiate da Novembre 2011 (si è passati dal dataset GHCN-M versione 3 a versione 3.1.0) perché è stato cambiato il software con lo scopo di correggere errori di codifica e per aumentare l’efficienza a run-time. Nella solita pagina sul mio server, oltre alla pagina NOAA citata ho riportato anche un paio di articoli relativi a questo importante cambiamento. Queste pagine non le conoscevo al momento di scrivere il post ma credo che modifichino poco le conclusioni: le modifiche partono da novembre 2011 (penso significhi che sono incluse nel file di anomalie “fino a” novembre 2011) ma la cosa che conta è il trend crescente tra dicembre e gennaio, indipendentemente dalla temperatura di riferimento che è la stessa per entrambe le serie.
Non ho ancora pensato abbastanza all’effetto che questo cambiamento potrebbe avere sulla diminuzione del gradiente ma credo che la cosa migliore da fare sia quella di aspettare la nuova anomalia di febbraio (uscirà tra qualche giorno) e vedere il comportamento rispetto a novembre ed eventualmente rispetto a dicembre, se si può pensare che novembre faccia ancora parte del vecchio dataset (farò la prova ma, per quello che dicevo prima, non credo cambi qualcosa).
Tu dici “L’ipotesi di un algoritmo che “ricostruisce” i dati delle misurazioni, spero con tutto il cuore, resti solo tale (per il bene della scienza, ovviamente).”.
Su questo punto non sono del tutto d’accordo: i dati mondiali sono molto diversi tra loro e presi in condizioni molto variabili. Devono essere omogeneizzati (non “massaggiati” alla Mann, per carità!) ad esempio per tenere conto dell’ambiente naturale attorno alla stazione e quindi gli algoritmi devono “ricostruire” il dataset. Ho trovato il sito dove sono a disposizione i dati grezzi (non ricordo dove, però sono partito dalla pagina NOAA di cui sopra) ma sono praticamente inutilizzabili da un singolo, senza strutture di supporto. Ovvio che la ricostruzione deve essere credibile – poi si può sbagliare e correggere i dati, non ci sono problemi in questo – e nel caso dei dati NOAA il confronto con altre serie di dati fa ragionevolmente pensare che lo sia.
Ciao
Franco
Il problema, secondo me, deve ricercarsi nella Tr. Da quello che ho potuto capire la Tr viene calcolata in automatico e cambia ogni qualvolta il file viene aggiornato. Nell’istante in cui la si blocca in una data ben precisa, tutto il sistema si imballa e si manifestano le anomalie citate nell’articolo. A questo punto sorge il problema di come calcolare questa Tr. Essa dovrebbe essere, sempre se ho capito i termini del problema, una sorta di “temperatura media” relativa ad un certo periodo. Se il periodo cambia (perché si aggiungono nuovi dati relativi a rilievi successivi) sembrerebbe logico che cambi anche la Tr (verrebbe calcolata, infatti, su un nuovo set di dati). Se, invece, Tr resta costante non terrà conto degli ulteriori dati aggiunti. Quale procedimento è corretto?
Procedendo per analogia con altre situazioni si dovrebbe calcolare una media relativa ad un periodo ben preciso e calcolare le anomalie rispetto a quel particolare valore (come si fa per la superficie dei ghiacci marini, per esempio). E’ pur vero, però, che in altre circostanze la media si calcola su tutti i valori delle misurazioni prese in considerazione.
Questo, ovviamente, se Tr può essere considerata una temperatura media, in caso contrario ciò che ho scritto risulta poco sensato 🙂 .
L’ipotesi di un algoritmo che “ricostruisce” i dati delle misurazioni, spero con tutto il cuore, resti solo tale (per il bene della scienza, ovviamente).
Ciao, Donato.
Il comportamento dei dati evidenziato da F. Zavatti è veramente singolare. Mi propongo di ritornare sull’argomento dopo averlo approfondito. Grazie, comunque, per aver evidenziato questa interessante “anomalia”.
Ciao, Donato.