di Franco Zavatti
______________________________________________________________________________
In questo post cerco di definire alcune procedure adatte ad identificare i Break-Point (BP) presenti in un dataset. In teoria i BP identificabili sono tutte le situazioni di salto improvviso o cambio di pendenza nei dati ma, con questa definizione, i BP che si possono trovare nei dataset climatici, affetti da forte rumore, sarebbero moltissimi e praticamente inutilizzabili. In realtà si cercano punti di discontinuità “epocale” nei quali le successive condizioni delle variabili climatiche cambiano sostanzialmente e che in qualche modo identificano l’inizio di un regime climatico diverso. Il numero di questi break point che chiamerò “Principali” (BPP) non dovrebbe essere superiore a 3-4 in un periodo di 120-140 anni (circa 1 BPP ogni 30-35 anni, ma dipende dal tipo di dataset).
Usando lo stesso criterio chiamerò i break point identificati tra due successivi BPP, “Secondari” o BPS.
Un esempio di BPP e BPS si vede in Fig.1 (pdf) dove si utilizza il dataset NOAA delle temperature medie mensili globali (terra+oceano) fino ad agosto 2013. Di questo dataset si usano le medie annuali.
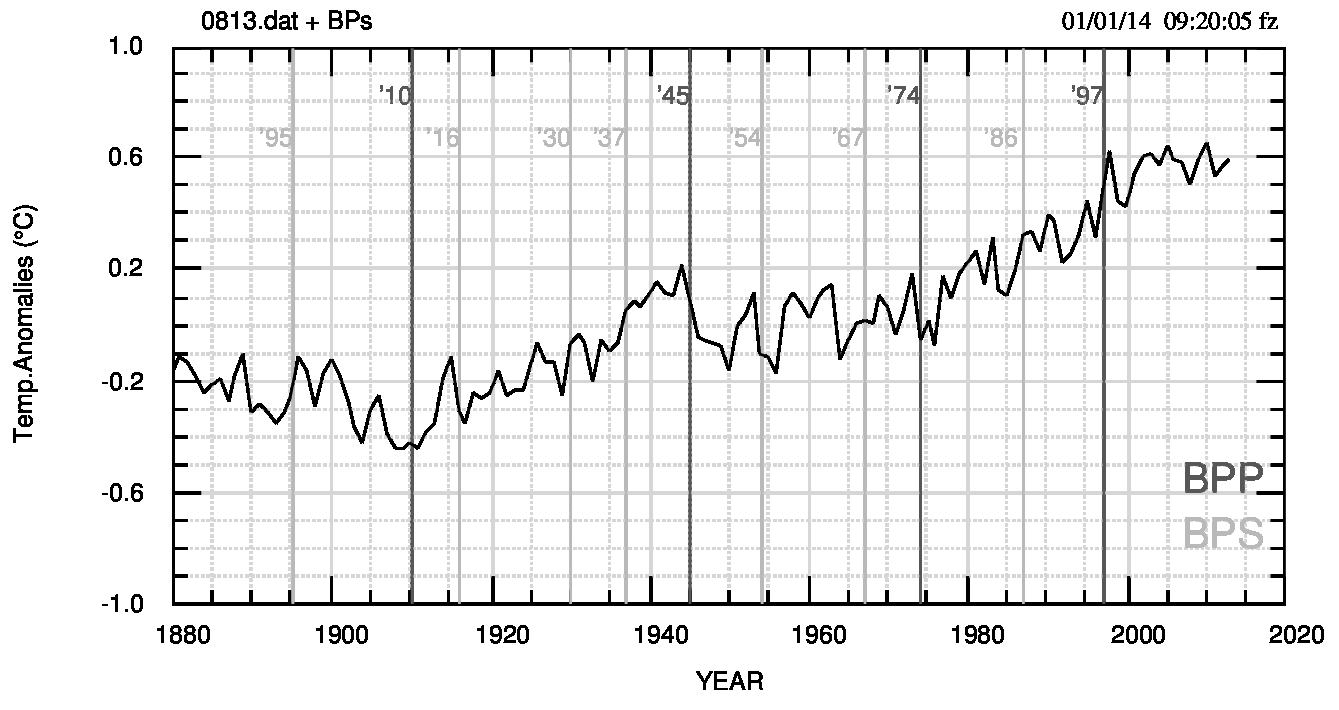
L’uso delle derivate
Un sistema immediato per trovare forti e improvvisi cambiamenti di pendenza è quello di calcolare le derivate numeriche punto per punto, ordinarle -eventualmente in modulo- selezionare le prime e le ultime 6 o 7 (dipende dal tipo di ordinamento) e, alla fine, confrontarle visualmente con il grafico del dataset (Fig.1). Questa tecnica fornisce tutti i breakpoint principali visibili all’esame visuale più i BPS dai quali sarà però necessario selezionare i più significativi. Un esempio si vede nella Fig.2 (pdf).
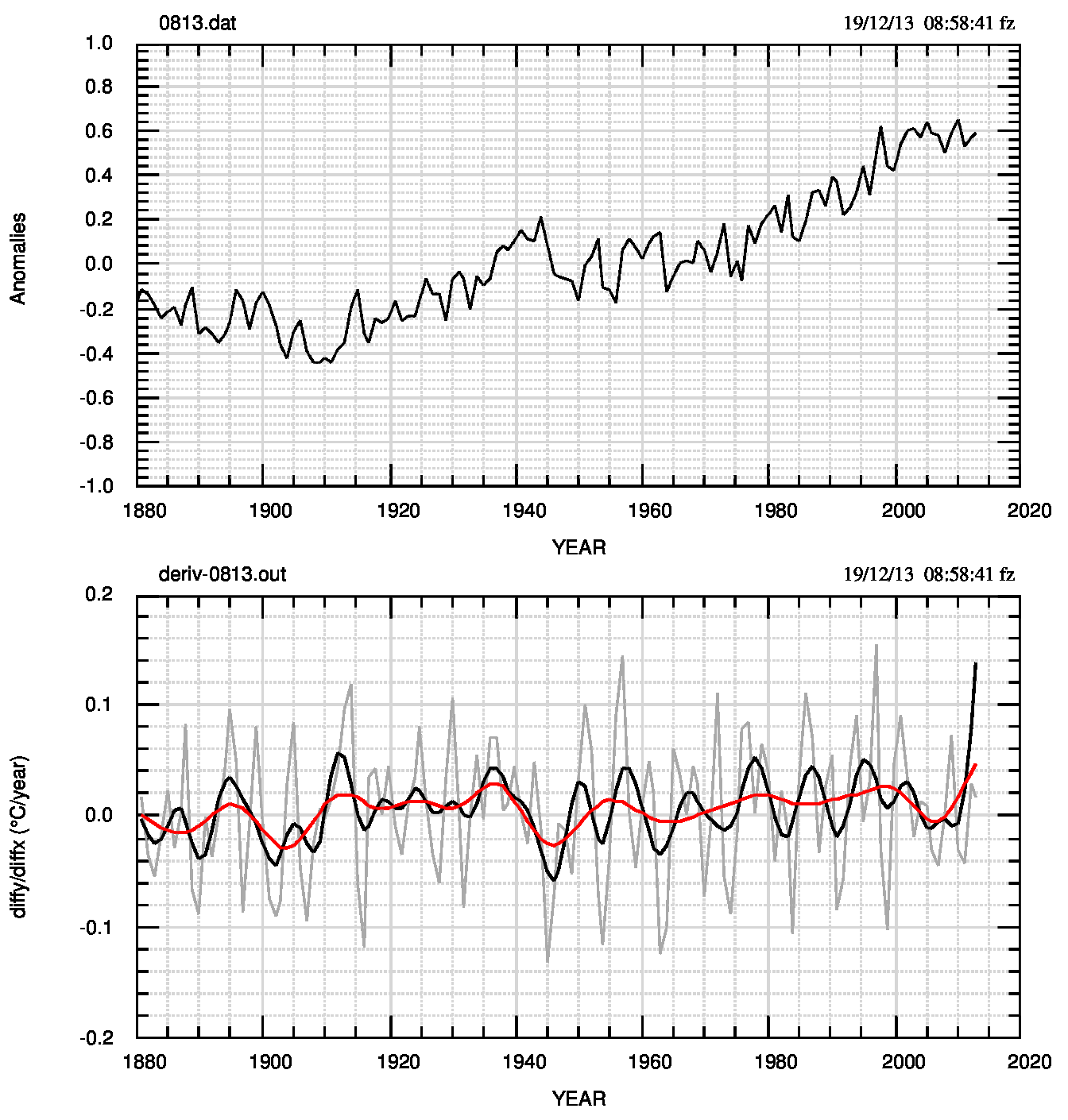
Tutto l’insieme può sembrare troppo soggettivo, e probabilmente lo è, ma esiste almeno un esempio (Zeileis et al, 2003, fig.8) in cui il Bayesan Information Criterium (BIC, criterio oggettivo) fornisce, per il metodo di Bai e Perron (2003), zero BP mentre gli autori ne selezionano due in base all’analisi dei dati e a considerazioni che, nel loro contesto, possono essere considerate soggettive (crisi petrolifera del 1973 e introduzione nel Regno Unito dell’obbligo delle cinture di sicurezza nel 1982). Quindi, la soggettività può essere un problema ma non sempre e comunque e con il metodo delle derivate “l’arbitrio” consiste nel decidere di non considerare significativo un BP che esiste ed è stato individuato dal metodo ma che, ad esempio, mal si accorda con lo scopo dello studio. Così, nel caso descritto qui, avendo osservato cambiamenti di regime con passo di circa 30 anni, si sceglieranno come BPP i BP a passo 30-35 anni, trascurando quelli a passo di circa 6-10 anni che pure sono individuati e visibili in Fig.1.
Dal punto di vista numerico, il metodo delle derivate consiste nel calcolare la grandezza deriv(i)=diff(Yi)/diff(Xi), dove le differenze diff(⋅) sono calcolate (se N è il numero dei dati)
avanti (forward) con
- (Y1-Y2), …, (YN-1-YN), dati da 1 a N-1, perdendo l’ultimo valore;
indietro (backward) con - (Y2-Y1), …, (YN-YN-1), dati da 2 a N, perdendo il primo valore;
centrali (central) con - (Y3-Y1), …, (YN-YN-2), dati da 2 a N-1, perdendo il primo e l’ultimo valore valore che sono calcolati con 1. e 2. rispettivamente.
L’uso delle derivate può essere applicato anche ai parametri statistici calcolati dai fit lineari descritti nel prossimo paragrafo.
L’uso del fit lineare
Il metodo consiste nel calcolare fit lineari di parti del dataset con dimensioni crescenti (come in questo grafico), a partire dal primo valore disponibile, assumento come tasso di crescita il passo del dataset. Poi si analizzano alcuni parametri (qui tre: l’errore quadratico medio (eqm o rms), il coefficiente di correlazione (cc) e la pendenza (α) della retta interpolante) per cercare una situazione estrema concomitante, o tale per almeno 2 dei 3 parametri, del tipo “eqm minimo; cc massimo, α massima”, dove minimo e massimo possono essere relativi e non necessariamente assoluti. L’ascissa corrispondente alla situazione descritta identifica quale punto della sequenza -e, con un semplice confronto, quale anno- coincide con il cambiamento. A questo valore dell’ascissa (o anno) si assegna la qualifica di 1.o break-point (sarà un BPP) e lo si usa come punto iniziale del secondo segmento, da cui ripetere la sequenza di fit lineari. Si cerca nuovamente il punto di massimo cambiamento, lo si identifica come 2.o BP e si ripete di nuovo la sequenza fino al termine dei dati.
I tre parametri di interesse si possono raccogliere insieme, per ogni segmento (cioè per i dati tra due BPP successivi), per un confronto immediato come nella Fig.3 (pdf).

o nel file bai.dat (sito di supporto) che raggruppa i valori numerici, o anche nella Fig.4 (pdf), in cui all’ascissa di Fig.3 è stato sostituito l’anno.

Nella Fig.3 i tre quadri rappresentano i parametri statistici scelti, in funzione del numero d’ordine delle osservazioni all’interno di ogni segmento di cui un BPP è l’inizio. La figura va letta verticalmente, segmento per segmento (o colore per colore) alla ricerca di almeno due situazioni estreme concomitanti. A volte la lettura è resa difficile dalla presenza dei quadrati pieni che hanno lo scopo di mostrare come i singoli segmenti non siano coperti in modo uniforme dai fit e che quindi questo metodo è suscettibile di ulteriori miglioramenti. La lettura è più agevole nella Fig.4 dove i segmenti sono meglio separati e l’ascissa è immediatamente fruibile: un esempio dei vantaggi della Fig.4 si può leggere nello scambio di commenti che ho avuto con Donato Barone qui a proposito dell’incapacità del metodo dei fit lineari di identificare il 4.o BPP (in generale, l’ultimo BPP). Mi ero convinto di questo, leggendo una versione precedente della Fig.3 e trascurando la Fig.4 che pure avevo già disegnata ma non capita bene.
Infatti, proprio da questa figura (e dal file numerico) si nota un massimo relativo sia per l’errore quadrato medio (rms) che per la pendenza in corrispondenza dell’anno 1998 (punto 24 del quarto segmento, in Fig.3) e un minimo relativo corrispondente al precedente anno 1997. In base ai criteri usati, il 1997 dovrebbe essere l’anno di inizio del 4.o BPP. Osservando con maggiore attenzione, si nota che i punti precedenti al 1997 si dispongono su un “plateau” di minimi relativi e che la pendenza (slope) raggiunge un valore minimo nel 1993 (punto 19 in Fig.3), per cui si potrebbe ipotizzare un cambiamento precedente al 1997. La presenza negli stessi anni de El Niño più forte mai registrato forse nasconde l’inizio di un regime climatico diverso o forse ne è la causa.
Per tentare di usare il metodo del fit lineare in modo più oggettivo si calcolano le derivate numeriche dei parametri statistici all’interno di ogni segmento e si selezionano le ascisse per cui le derivate sono nulle (come in Tab.1 sul sito di supporto) per almeno due parametri. Questo può essere fatto graficamente, utilizzando la Fig.5 (pdf).

Dalla Fig.5 (e dai suoi ingrandimenti), gli estremi per ogni segmento dati dalla tabella
| 1.o seg. | 14 1893 |
21 1900 |
33 2007 |
40 1919 |
| 2.o seg. | 21 1933 |
31-32 1944 |
||
| 3.o seg. | 18 1962 |
28 1972 |
32 1976 |
|
| 4.o seg. | 11 1985 |
25 1999 |
33 2007 |
35 2009 |
sembrano essere più incerti rispetto a quelli trovati con gli altri metodi ma sono spesso vicini a quelli (1-2 punti prima o dopo). Il primo pensiero è che la chiave di lettura dei grafici di Fig.5 debba ancora essere chiarita.
NB: tutti i dati, le immagini e le tabelle sono disponibili sul sito di supporto a questo link
___________________________
29.1.14. Aggiornamento
Dopo aver spedito questo post c’è stata un’evoluzione: quanto descritto è utile ad identificare i BP (sia i principali, BPP, che i secondari, BPS). Poi, per valutare la veridicità dei BP trovati sia con i fit a dimensione crescente che con le derivate, si usa il test di Student (t-test) applicato alle pendenze (p1 e p2) dei fit per il segmento precedente il BP e per il successivo. Viene testata l’ipotesi nulla Ho:p1=p2 e se il livello di confidenza è basso (cioè è alta la probabilità dell’ipotesi alternativa H1:p1≠p2) il break point in esame viene considerato reale (significativo). Se il test sulle pendenze mostra un’alta confidenza nell’ipotesi nulla (cioè le pendenze sono statisticamente uguali) il test di Student viene applicato alle medie aritmetiche dei due segmenti per verificare se il BP separa due segmenti di uguale pendenza ma diversa media (un caso simile a quello pubblicato da Luigi Mariani su CM qui, fig.1). Quindi si verifica l’ipotesi Ho:m1=m2, con m1 e m2 medie del segmento che precede il BP e del segmento che segue il BP, rispettivamente. Se il livello di confidenza per Ho è alto, il BP viene considerato non significativo e in pratica rigettato.
Di seguito un esempio di applicazione relativo alle anomalie medie annuali di temperatura del set CONUS (CONtiguous U.S.) statunitense (i dati originali qui; vedere anche il blog di Steven Goddard, qui). I fit parziali mostrano BPP e BPS negli anni 1911, 1930, 1951, 1977, 1985, 1993, 1997 (tutti con un’incertezza di ±1 anno). Dal test di Student sulle pendenze, utilizzando i dati della tabella, si ricava:
(**) t-test per le medie |
Come si vede, i primi quattro BP sono molto significativi mentre quello relativo al 1911 è significativo al 28.5% sulle pendenze e all’11% sulle medie e quindi viene scartato. |
___________________________
Bibliografia
- Tutti i grafici e i valori numerici si trovano nel sito di supporto qui.
- Bai J., Perron P.: Computation and Analysis of Multiple Structural Change Models, Journal of Applied Econometrics, 18, 1-22, 2003.
- Hansen, B.E.:The New Econometrics of Structural Change: Dating Breaks in U.S. Labor Productivity, Journal of Economic Perspectives, 15, n.4, 117-128, 2011. pdf
- Matlab DIFF:Numerical Differentiation pdf
- Perron P.: Dealing with structural changes, Prepared for Palgrave Handbook of Econometrics, Vol. 1: Econometric Theory, 2005. pdf
- Zeileis A., Kleiber C., Krämer W., Hornik K.: Testing and dating of structural changes in practice , Computational Statistics & Data Analysis, 44, 109-123, 2003. pdf
- Zeileis A., Shah A., Patnaik I.:Testing, Monitoring, and Dating Structural Changes in Exchange Rate Regimes , Computational Statistics & Data Analysis , 54(6),1696-1706, 2010. doi:10.1016/j.csda.2009.12.005 pdf


Sii il primo a commentare