di Franco Zavatti
______________________________________________________________________________
Nell’aggiornamento dei dati NOAA a novembre 2013 ho ricalcolato gli spettri mem dei primi tre mesi per i quali dispongo di dati (novembre 2011, dicembre 2011, gennaio 2012) e ho notato che con i nuovi spettri il periodo cresce linearmente mese dopo mese e quindi con il numero dei dati (cioè con il numero di poli npoli che uso come parametro per la MEM). Nasce quindi il sospetto di non poter studiare la supposta evoluzione temporale dei massimi spettrali (sia come periodo che come potenza) perchè in realtà sarebbe dovuta a fattori numerici. Per verificare il sospetto ho costruito un dataset sintetico usando una sinusoide (seno e coseno) + rumore gaussiano normalizzato, a media nulla e varianza unitaria, come nella Fig.1 (pdf)
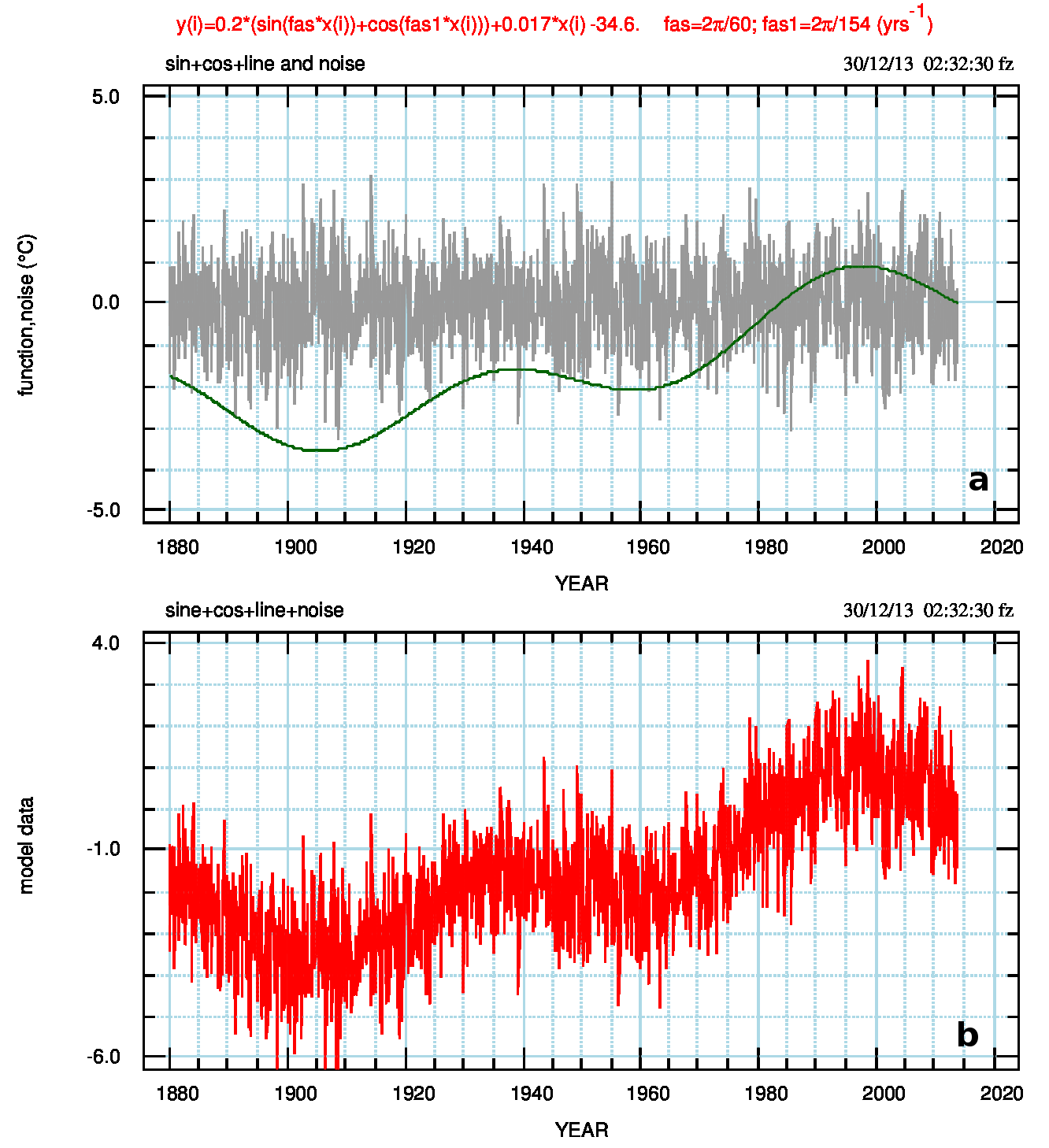
Di questo dataset ho calcolato gli spettri MEM cambiando:
- il numero dei punti, simulando in questo modo l’aggiungersi dei mesi. Ho usato N=1500, 1501, 1502, 1510, 1515, 1520 dati e ho calcolato la MEM nel modo per me usuale, con npoli=N/2.
- il numero dei punti, mantenendo costante il valore di npoli=750.
Bisogna notare che il caso reale del dataset NOAA è un po’ più complicato perché non ci si limita ad aggiungere il valore di anomalia del nuovo mese ma tutto il dataset viene modificato dalla procedura di omogenizzazione. Quindi ad ogni mese tutti i dati cambiano, seppur di poco (da qualche millesimo a qualche centesimo di grado; però le anomalie sono fornite al decimillesimo di grado), mentre nella simulazione i dati sono sempre gli stessi.
I risultati sono riassunti nelle prossime due figure. La prima -Fig.2 (pdf) – per npoli variabile e la seconda -Fig.3 (pdf) – per npoli fisso.
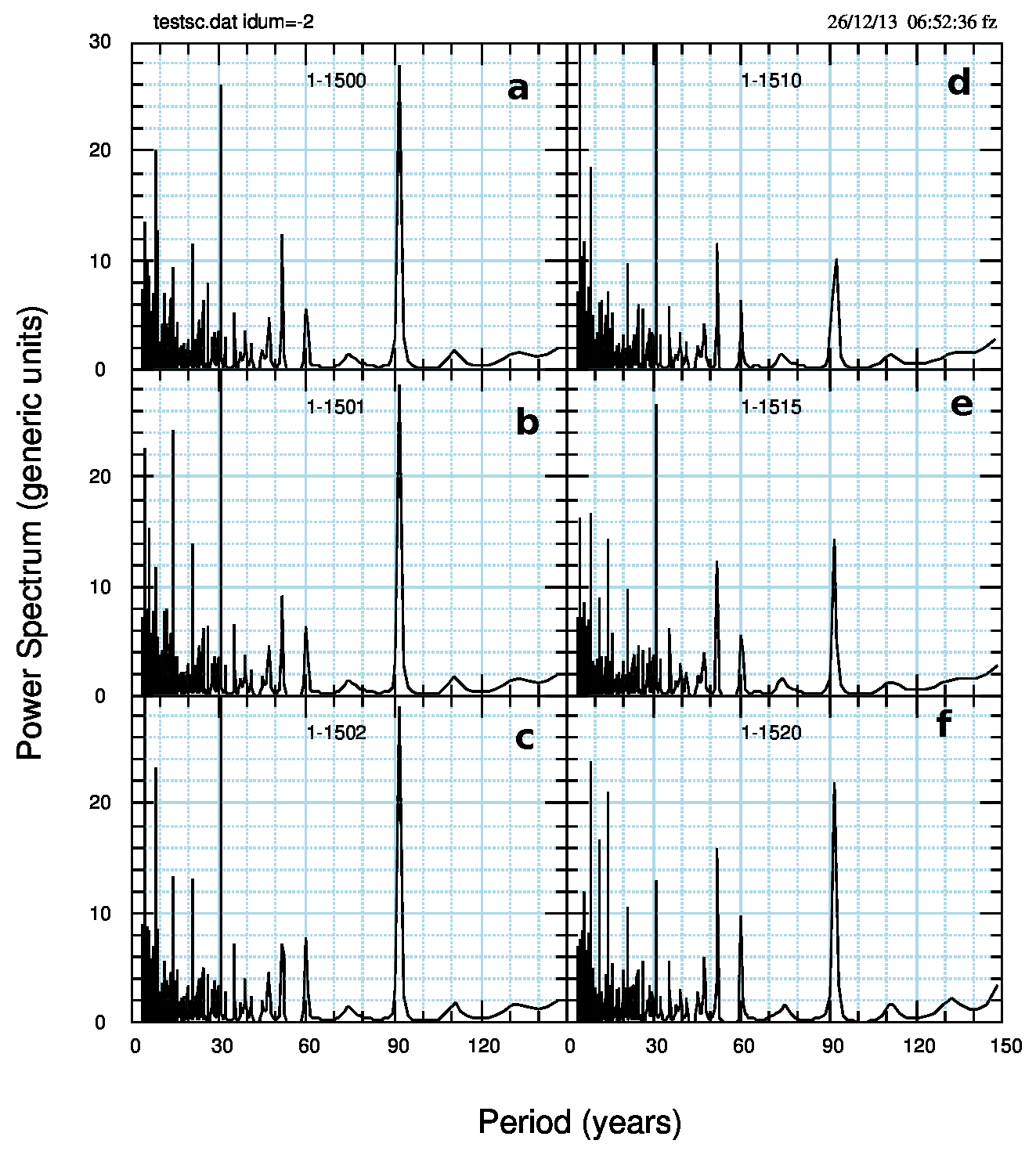
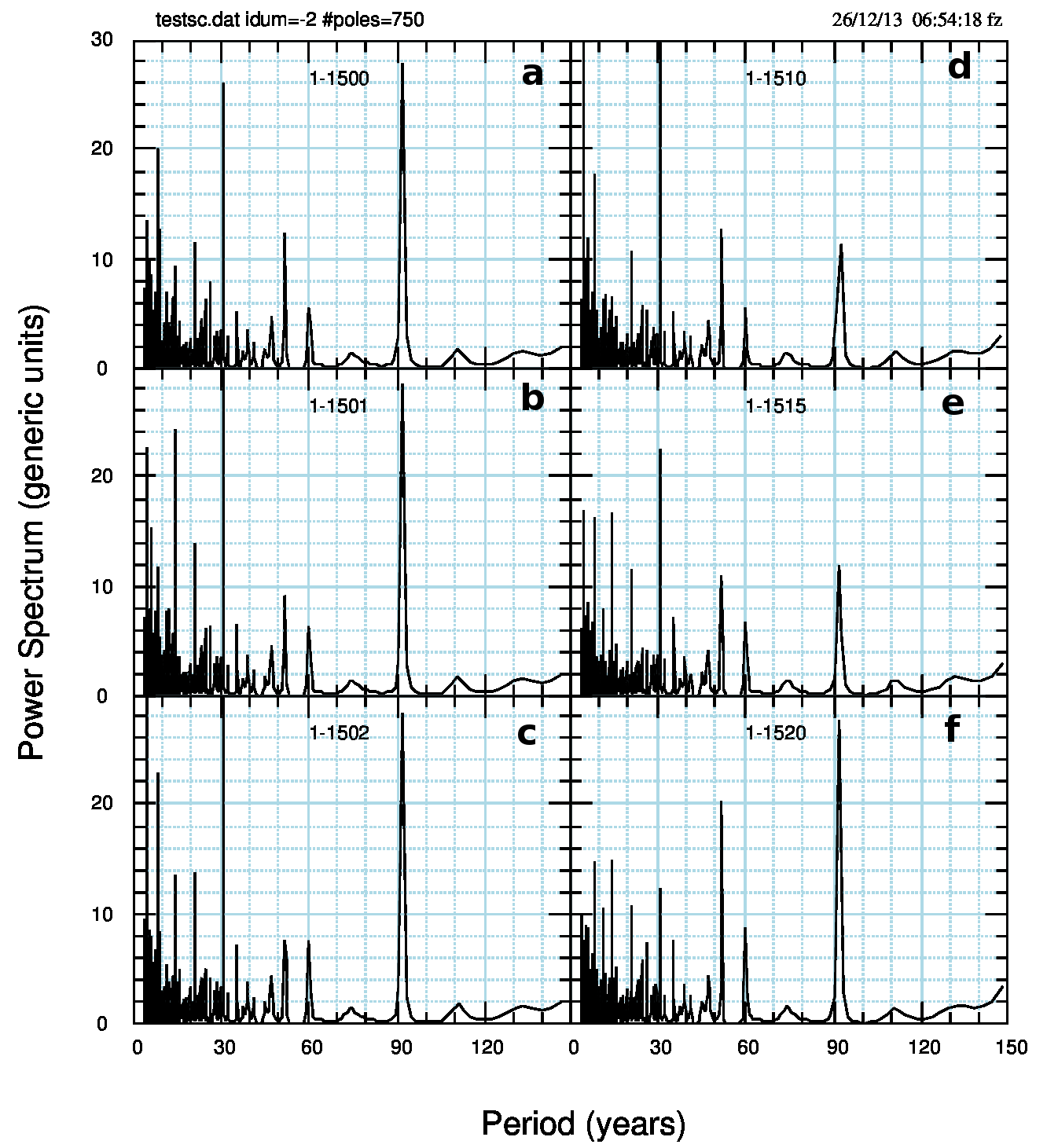
Anche al primo colpo d’occhio si notano due aspetti: il periodo dei vari picchi non cambia in modo visibile mentre le potenze cambiano notevolmente e non in modo proporzionale al numero dei punti. Poi, il passaggio da numero di poli variabile e fisso cambia poco la situazione tranne nel caso di 1520 punti dove si nota qualche differenza nei periodi minori e in generale nell’altezza dei massimi (per una visione d’insieme).
Una conferma di quanto affermato viene dalla Fig.4 (pdf) dove la potenza dei massimi è mostrata in funzione del numero di punti usati.
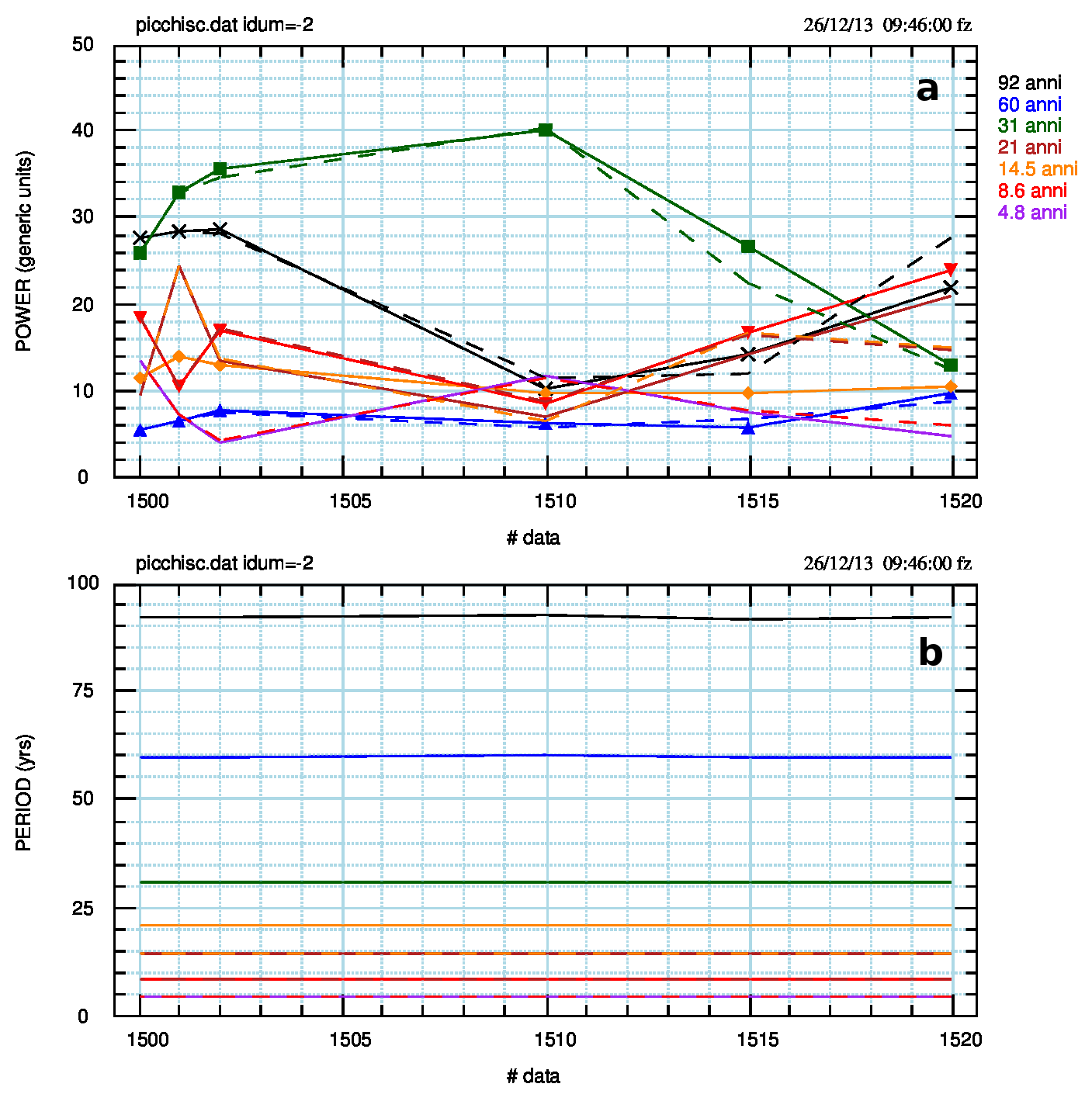
Per ogni massimo, le variazioni della potenza in funzione del numero di punti usati sono molto elevate e vanno da 30.1% a 70.5% con npoli variabile e da 22.2% a 72.7% per npoli=750, come si vede nella Tab.1. Questa variabilità di fatto preclude ogni possibilità di osservare una reale evoluzione temporale della potenza spettrale e di attribuire a questa variazione un significato fisico.
| Periodo (anni) |
%Potenza N/2 |
%Potenza 750 |
%Periodo |
|---|---|---|---|
| 92 | 64.2 | 64.2 | 1.19 |
| 60 | 42.8 | 35.3 | 0.33 |
| 31 | 67.8 | 69.2 | 0.33 |
| 21 | 30.1 | 22.2 | 0.20 |
| 14.5 | 70.5 | 72.7 | 0.18 |
| 8.6 | 64.0 | 53.2 | 0.12 |
| 4.84 | 45.3 | 54.6 | 0.08 |
Tab.1-Variazione percentuale della potenza e del periodo per ognuno dei massimi spettrali utilizzati. La tabella dice che, ad esempio, per il massimo di periodo nominale 14.5 anni, la potenza varia del 70.5% in funzione del numero dei dati, con npoli=N/2 e del 72.7% con npoli=750. Il periodo invece varia dello 0.18% (non c’è differenza tra i due valori di npoli).
Il quadro b) della Fig.4 mostra una sostanziale stabilità del periodo dei massimi spettrali in funzione del numero dei punti (in funzione del tempo nel caso reale), anche se la scala molto ampia non permette di apprezzare le pur piccole fluttazioni. Le fluttuazioni del periodo si vedono meglio nella Fig.5 (pdf).
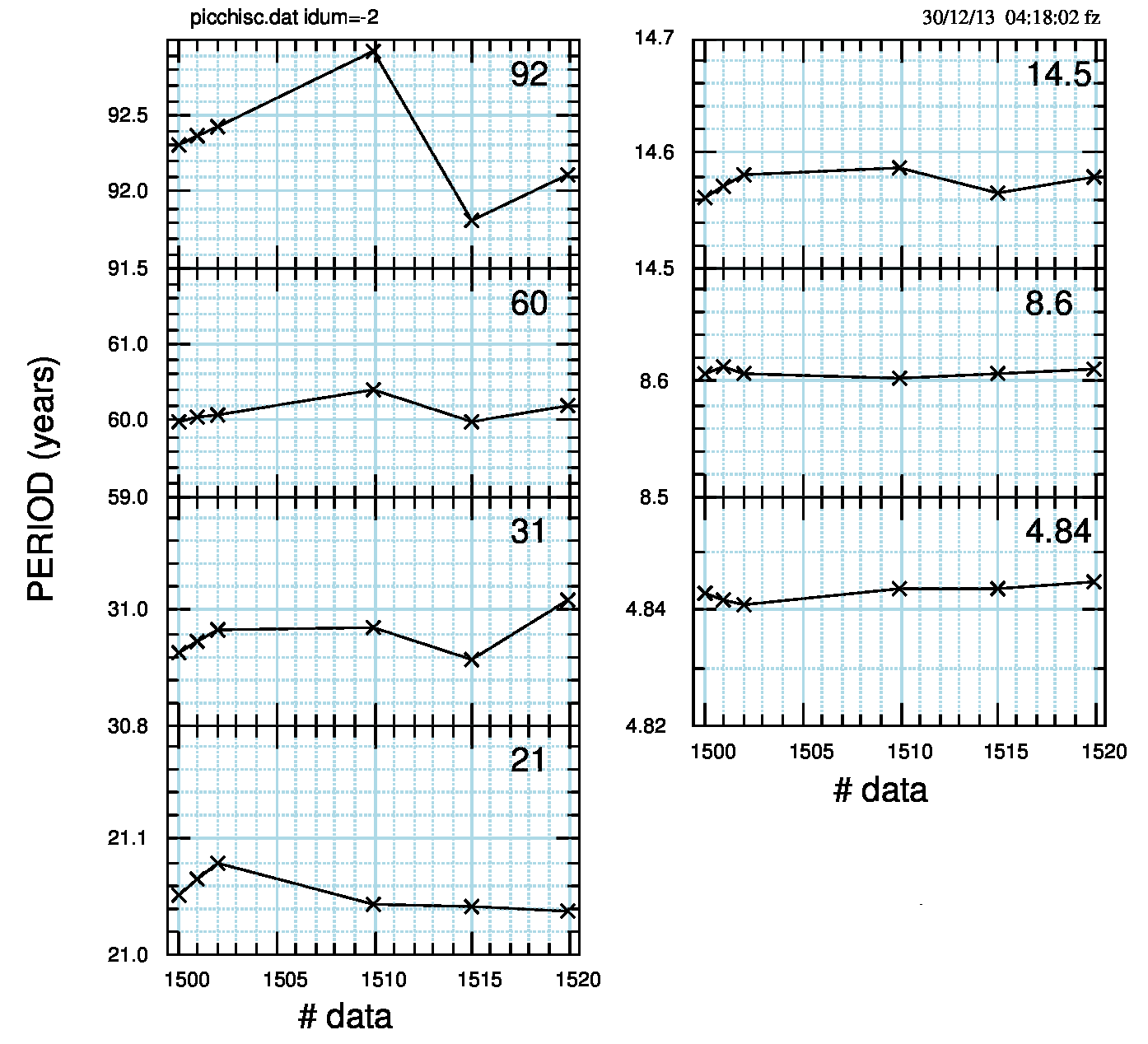
dove appaiono comprese tra 1.2% e 0.08%. In questa simulazione, quindi, i periodi sono sostanzialmente costanti rispetto al numero di punti (al tempo, nel caso reale) e al parametro npoli della MEM.
Da questa simulazione concludo che non ha molto senso discutere ancora i cambiamenti nel tempo dei massimi spettrali del dataset NOAA.
Modelli sintetici
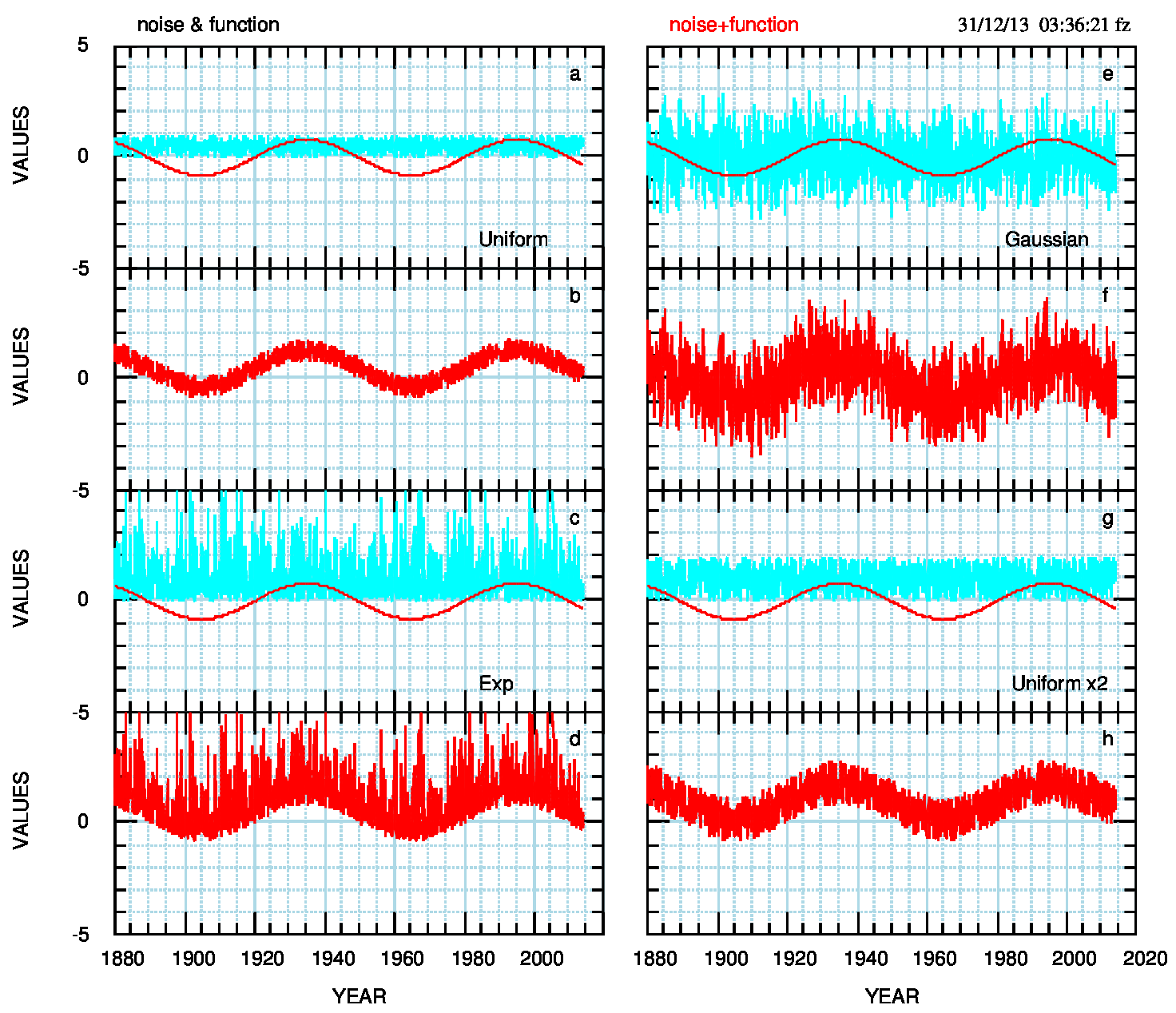
L’evoluzione naturale dei programmi usati per costruire la Fig.1 mi ha portato a scrivere codice per avere una maggiore varietà e flessibilità quando ho bisogno di costruire modelli sintetici adatti anche alle serie temporali climatiche. Il codice consiste nel comando Bongo NOISE che genera un file di rumore di tre tipi: gaussiano standardizzato (cioè con media nulla e varianza unitaria. Questo è il rumore usato abitualmente qui); uniforme (ogni valore ha la stessa probabilità di apparire dui tutti gli altri valori); esponenziale (positivo e di media uniutaria). Le tre funzioni di rumore disponibili appaiono insieme nella Fig.6 (pdf).
La seconda parte del codice è il programma fortran stand-alone (ma un qualsiasi programma eseguibile può essere “lanciato” dall’interno di Bongo, tramite il comando DOS) FUNC.F che genera una funzione analitica, permettendo la scelta tra 5 tipi di ascissa -tra cui anno.mese/12 (per medie mensili) e anno (per medie annuali), potendo scegliere l’anno iniziale- e 7 tipi di funzione, tra cui anche due funzioni particolarmente utili in climatologia (retta+seno e retta+seno+coseno) in quanto in grado di approssimare le serie di anomalie di temperatura fissando opportunamente i parametri.
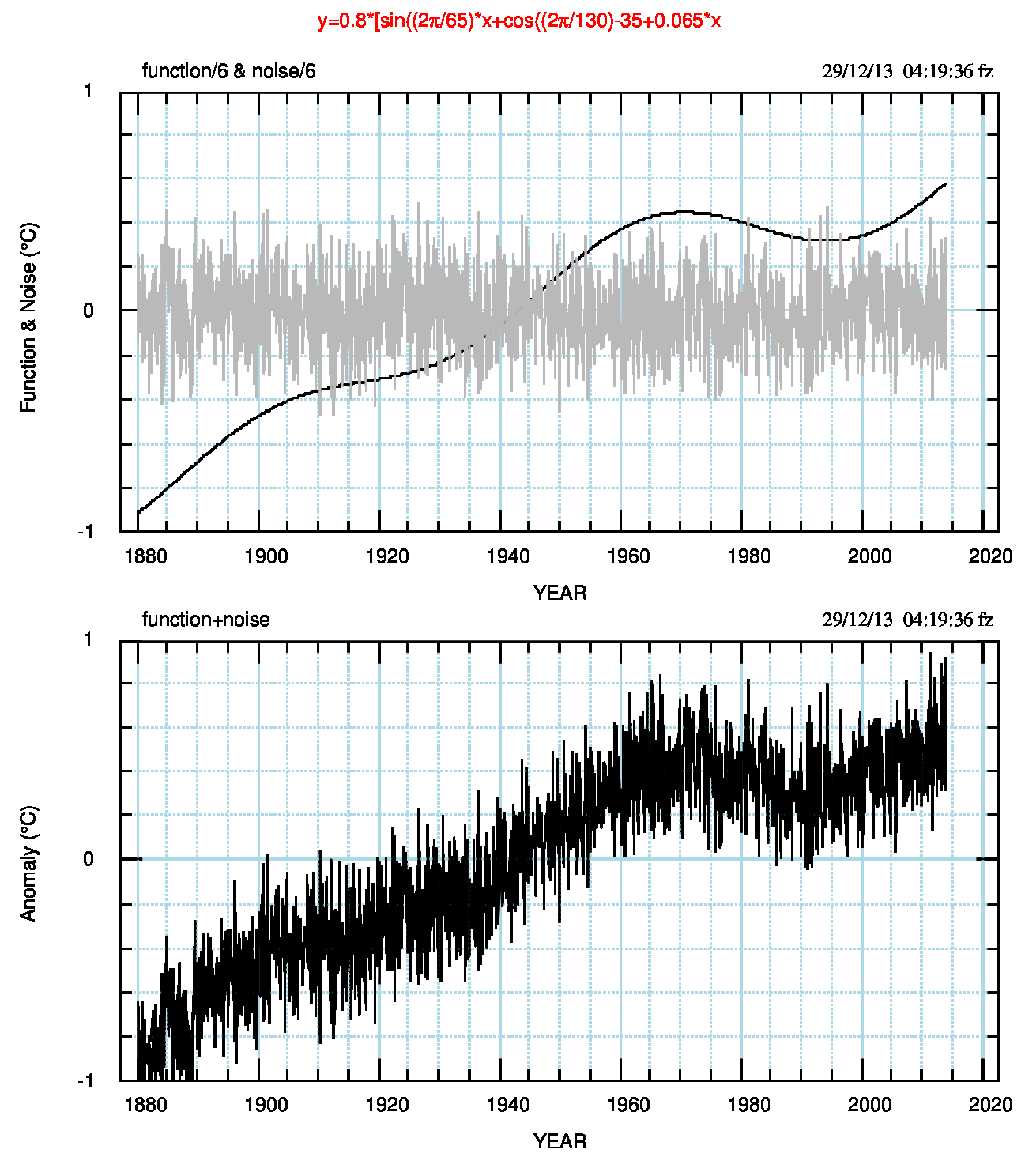
La terza parte del codice è il file di comandi Bongo FERR.BON che aggiunge il rumore alla funzione analitica scelta, scrive il file di output MODEL.DAT (nome che sarà opportuno cambiare in MODELx.dat, con x, da 1 a 7, numero della funzione scelta) e grafica il modello finale. Se serve, FERR.BON può essere sostituito da FERRPLOT.BON che, oltre alle operazioni di FERR.BON, grafica i dati nella forma della Fig.6 (rumore e funzione separati e poi uniti), come nella successiva Fig.7 (pdf).
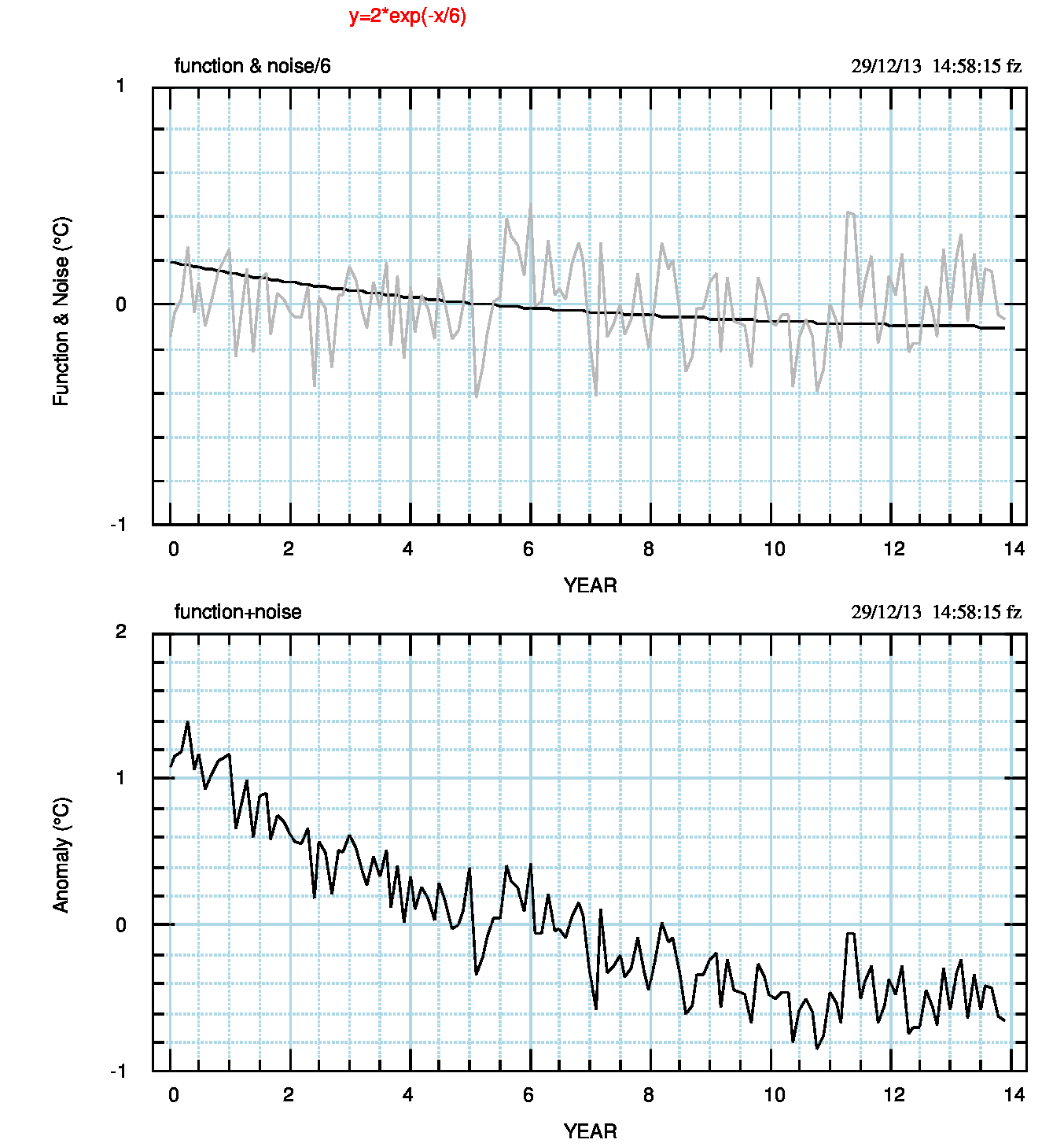
I valori numerici del modello sono disponibili come model5.dat nel sito di supporto. La Fig.8 (pdf) mostra un esempio in cui le ascisse sono in unità di 0.1 (qui chiamate “anni”) e riguardano i primi 140 punti del dataset. Questo modello potrebbe essere usato per studiare la presenza dei break-point e dei segmenti. I valori numerici del modello sono disponibili come model7.dat nel sito di supporto.
_________________________________
Bibliografia
- tutti i dati sono disponibili nel sito di supporto.
- Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes in Fortran, 2.nd Edition, Cambridge University Press India, 2009. ISBN 978-81-85618-17-3.


“Da questa simulazione concludo che non ha molto senso discutere ancora i cambiamenti nel tempo dei massimi spettrali del data set NOAA.”
.
Caro Franco sono d’accordo con te. I cambiamenti dei massimi spettrali al variare del tempo sono un artificio di calcolo connesso al metodo MEM e, in particolare, al numero dei poli e non trovano riscontri fisici.
Sulla base di quanto hai scritto, però, l’aggiunta di nuovi dati può solo introdurre significative variazioni nella potenza del periodo e non nel periodo stesso. Questo giustificherebbe le piccole variazioni dei periodi (periodi che entrano o escono dalle bande spettrali “astronomiche”) e “l’evoluzione” delle potenze dei vari periodi.
Ciò che invece, secondo me, non riesce a giustificare è la scomparsa di alcuni periodi che erano presenti nei dati prima dell’ultima omogeneizzazione e che sono scomparsi nell’ultima versione del data-set NOAA .
.
Chiudo con un grande grazie per il tuo lavoro certosino che ci ha portato a mettere un punto fermo su di una discussione che si trascinava da mesi: i periodi insiti nei data set possono considerarsi un dato di fatto, le variazioni nel tempo delle potenze di tali periodi, invece, rappresentano un artificio di calcolo. La conoscenza progredisce per piccoli passi (non sempre nella stessa direzione). 🙂
Ciao, Donato.
“Ciò che invece, secondo me, non riesce a giustificare è la scomparsa di alcuni periodi che erano presenti nei dati prima dell’ultima omogeneizzazione e che sono scomparsi nell’ultima versione del data-set NOAA.”
Caro Donato, questo è un’altro problema ma è un dato di fatto che la versione 3.2 del dataset NOAA è più stabile della precedente, con fluttuazioni entro un centesimo di grado per la maggior parte dei dati ed estremi entro 3 centesimi di grado per le parti, quelle iniziali, che mostrano maggiori differenze. Se questa stabilità è un segno di elaborazione “meno invasiva” posso solo (e voglio) sperarlo. Malgrado avessi deciso di non
pubblicare più i dati NOAA, proprio a causa della loro stabilità, pensavo di continuare ad elaborarli tutti i mesi e tenerli per me, in attesa di qualche cambiamento. Purtroppo forse non sarà possibile: infatti nel sollecitare l’aggiornamento del dataset ho scritto a J.M. Kobar di NOAA e ho ricevuto questa risposta (il 31 gennaio scorso):
Hi Franco,
The December 2013 temperature anomaly is now updated on the ftp site. I have been told that this ftp site is eventually going away and you can find these files through the Global Climate at a glance website at the following url:
http://www.ncdc.noaa.gov/cag/time-series/global
Have a good day.
Ho dato appena un’occhiata al nuovo sito e mi è sembrato di vedere che ora i dati sono raggruppati per mesi (tutti i “gennaio” dal 1880 ad oggi; tutti i “febbraio”, ecc). Se è così, sarò obbligato a molto lavoro in più per avere un dataset come quello precedente, e i nuovi dati hanno solo due cifre decimali e non più quattro. E poi non ho ancora capito se nel nuovo sito c’è il “ricalcolo” di tutto il dataset o solo l’aggiunta dell’ultimo dato.
Vedrò (i dati CONUS del post sui break point li ho scaricati dallo stesso sito e vanno bene …), ma credo che abbandonerò il dataset se non riuscirò a capire questi aspetti.
Ciao. Franco
“questo è un’altro problema”. Mi è scappato l’apostrofo chiedo scusa.
Come mi dicevano da bambino, un asino non si apostrofa e un’oca sì, con riferimento agli alunni somari e alle alunne oche (nessun riferimento ai pennuti credenti che allora sicuramente non esistevano).