Le due parti precedenti le trovate qui e qui, poi, a breve, sarà disponibile un documento in pdf per il download di tutto il lavoro. Questo post resterà in evidenza per qualche giorno, quelli che seguiranno li trovate subito sotto.
gg
[line style=”normal”][/line]
Nella terza parte ci apprestiamo a ricercare le possibili cause del riscaldamento globale che ha interessato il nostro pianeta a partire dalla metà del 1850 e più segnatamente dai primi anni del XX secolo. Premetto che sono solitamente molto restio nel trattare la variabile temperatura per diverse ragioni. La prima riguarda la non chiara attendibilità oggettiva dovuta al diverso trattamento dei dati, tanto che nei data-set disponibili si riscontrano anche notevoli differenze. La seconda è dovuta alla spesso difforme classificazione secondo gli standard WMO delle stazioni di rilevamento con la loro reale ubicazione, la distribuzione areale delle stesse essendo concentrata in massima parte nell’emisfero boreale e nella fascia delle medie latitudini degli USA, Europa e Asia orientale. Per il resto, in assenza di dati certi, si usano tecniche matematiche di interpolazione e omogeneizzazione.
Comunque se le precedenti motivazioni hanno un effetto sull’ampiezza delle singole oscillazioni nel breve periodo e scarso nelle oscillazioni di lungo periodo, la variabile temperatura esprime in ogni caso l’effetto di una variazione e non la sua causa, per cui se vogliamo indagare sulle motivazioni che l’hanno generata dobbiamo concentrarci nella ricerca delle cause. Quando abbiamo la febbre questa non rappresenta mai la causa dell’infezione bensì il suo effetto. Agire sul sintomo senza capirne le cause non produce alcun effetto significativo reale verso la guarigione, piuttosto produce uno spreco di risorse e forse anche di preziose energie. Senza conoscere le dinamiche che da sempre hanno impresso nel sistema climatico quelle “cause” che hanno prodotto la naturale variabilità climatica, non sarà possibile quantificare il valore aggiunto della variabile antropica, sempre che ne abbia. Solo attraverso la conoscenza sarà possibile prendere le dovute decisioni. Quindi l’analisi del dato della variabile temperatura può essere utile come elemento di supporto nella ricerca della sua causa e non viceversa. Qualunque modello climatico attualmente in uso che non tenga conto delle molteplici cause naturali è a mio avviso da ritenersi poco utile. I dati ottenuti possono rappresentare un “caso di studio” puramente didattico e virtuale. Nella migliore delle ipotesi può, quindi, rappresentare uno dei possibili scenari climatici ma certo non può assumere il titolo di rappresentazione della realtà soprattutto se gli output corrono lungo gli estremi.
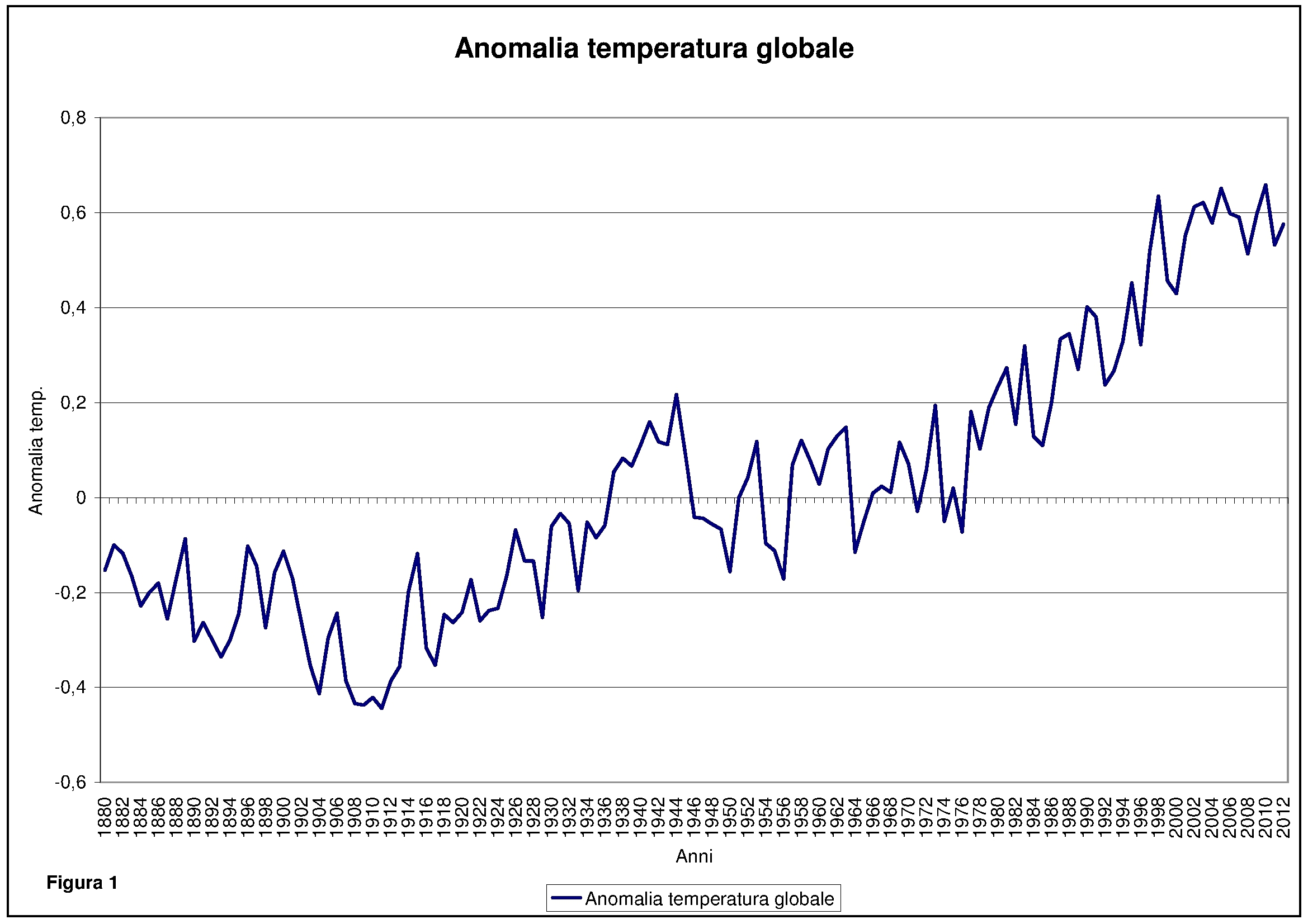
Dopo questa lunga premessa continuo nell’enunciare la ricerca compiuta verso l’individuazione dei segnali naturali alla base della risposta climatica terrestre. In figura 1 riproponiamo il grafico della variabile anomalia della temperatura globale secondo il data-set dell’NCDC e già commentato nel primo articolo.
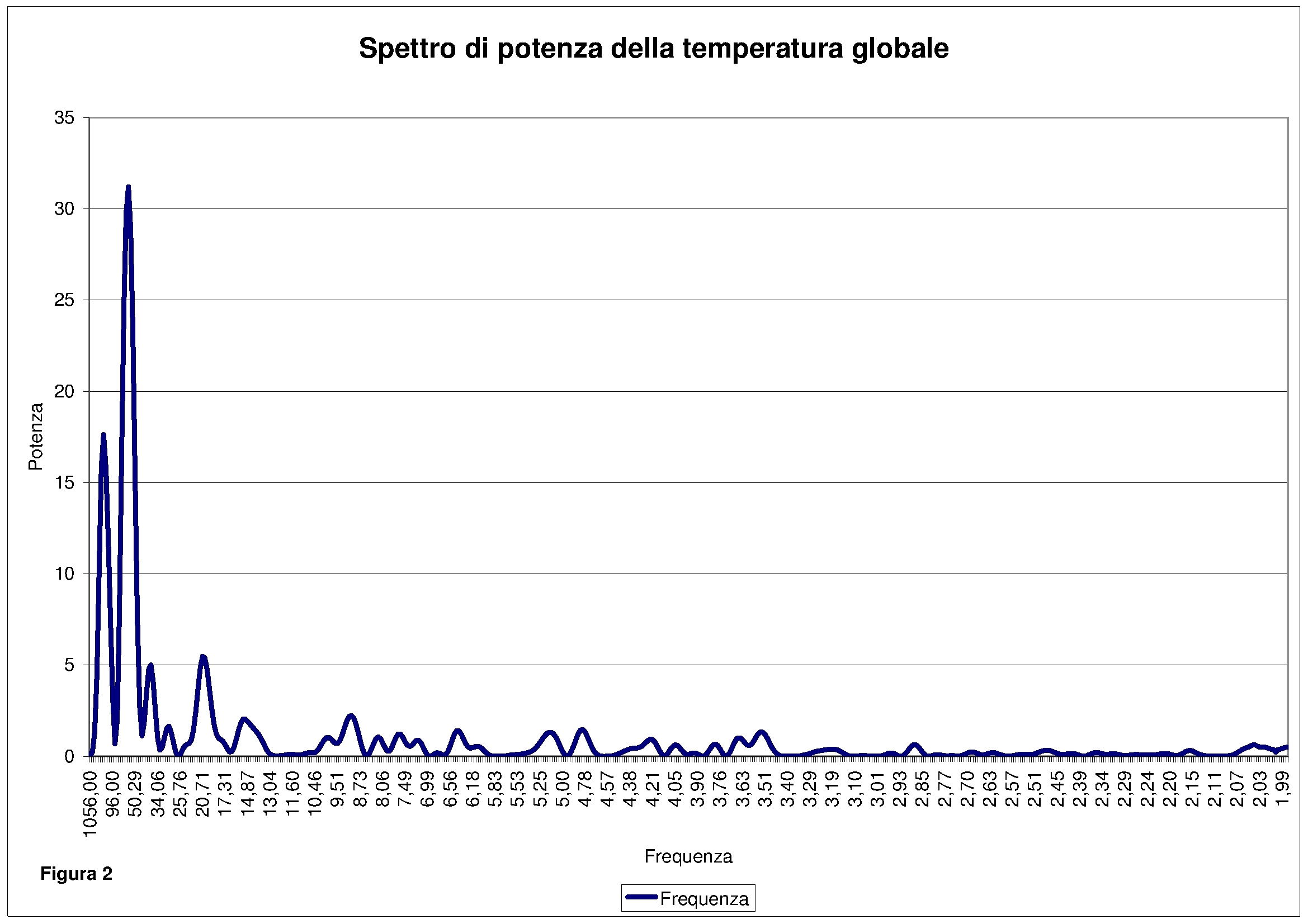
Benchè il campionario disponibile dei dati sia ancora insufficiente per individuare segnali a più bassa frequenza si è comunque proceduto a sottoporre il data-set ad analisi spettrale, vedi grafico in figura 2, evidenziando una serie di segnali a bassa frequenza su cui avviamo un’indagine.
L’analisi dello spettro ci suggerisce delle fasce di frequenza su cui sembra modularsi il segnale della temperatura. Di seguito si elencano le fasce di frequenza suddivise per gruppi:
- compresa tra i 352 e 90 anni con un picco attorno ai 150 anni;
- compresa tra circa 75 e 48 anni con picco attorno ai 59 anni;
- compresa tra 42 e 34 anni con picco a circa 38 anni;
- compresa tra circa 31 e 27 anni con picco attorno ai 30 anni;
- compresa tra circa 22 e 19 anni con picco a circa 21 anni;
- compresa tra circa 16 e 13 anni con picco sui 15 anni;
- compresa tra circa 12 e 11 anni con picco a quasi 12 anni (11,73);
- seguono gruppi di frequenze comprese tra i 3 e i 10 anni.
Il picco maggiore per tutti i gruppi sopra descritti si riscontra a 58,66 anni.
In questo studio fisseremo la nostra ricerca nel campo dei segnali a bassa frequenza superiori ai 22 anni. Questa scelta è dovuta a due motivi principali: il primo riguarda le note frequenze appartenenti ai gruppi 5° e 7° sopra descritti che si ritiene facilmente riconducibili all’attività solare e rispettivamente ai cicli noti di Hale e di Schwabe. Il secondo sarà meglio evidenziato nelle conclusioni di questa ricerca e quindi non lo anticipiamo. Ad una attenta analisi si nota come i segnali a più bassa frequenza godano di un ampio margine di segnale rispetto alle più alte frequenze e ritengo ciò sia dovuto al numero esiguo di anni costituente il data-set.
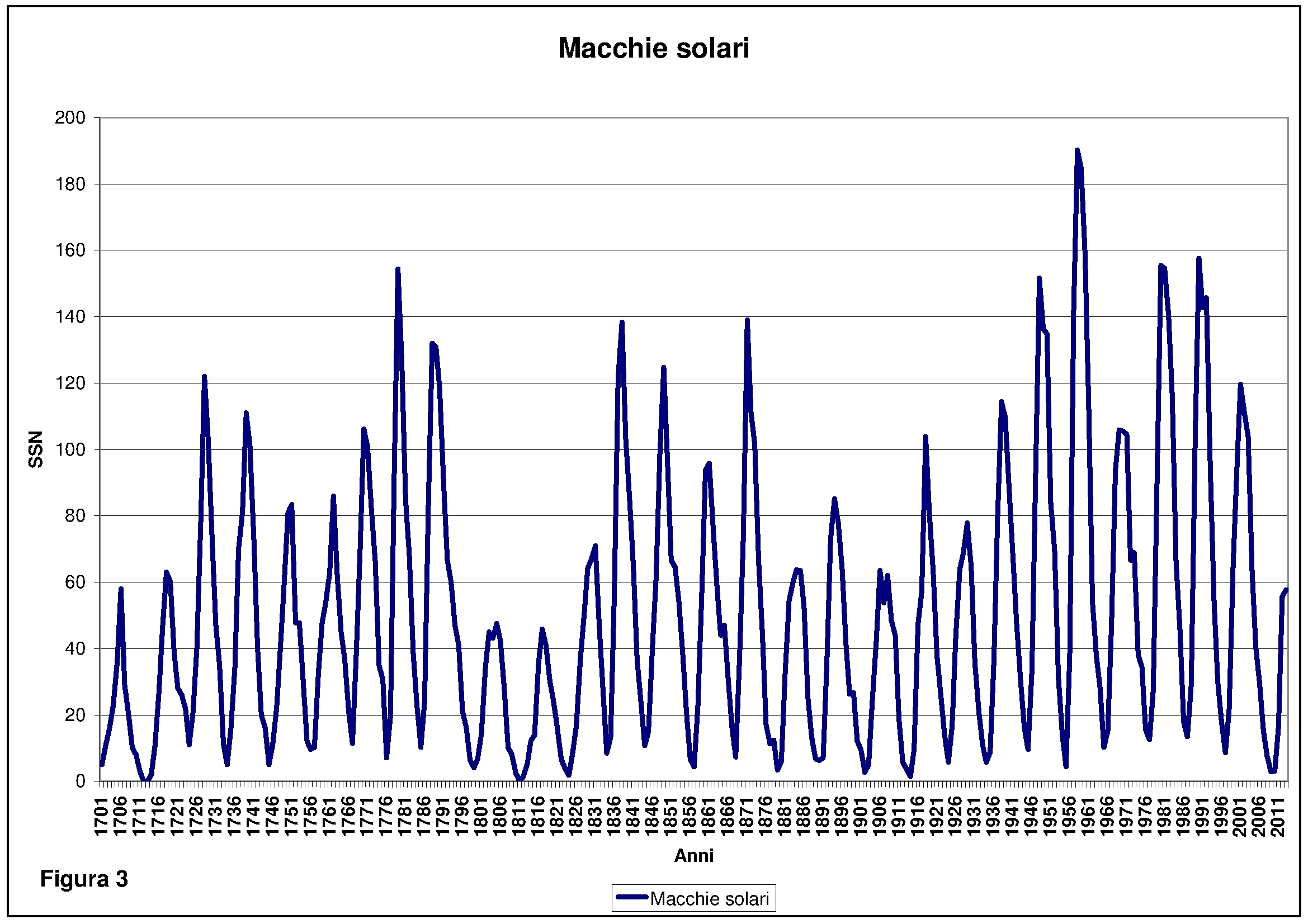
Il sistema climatico terrestre esiste perché la Terra ha un’atmosfera sufficientemente densa nella quale si sviluppano correnti orizzontali e verticali principalmente indotte dal gradiente termico innescato dalla diversa quantità di calore ricevuta dal sole al variare della latitudine. In mancanza del sole non vi sarebbe né clima e né vita sulla terra. Il sole non irradia in maniera perfettamente costante energia ma con modalità direttamente proporzionali al suo livello di attività. In questa ricerca tralasceremo tutti gli aspetti della fisica solare perché non oggetto di questo stesso studio ma ci soffermeremo sulla ricerca delle probabili cause che alterano l’attività solare. In figura 3 è visibile il grafico dell’attività solare espressa dal numero medio annuo di macchie solari a partire dal 1700 e fino al 2012.
Il grafico permette già a prima vista alcune considerazioni. Si notano tre periodi nei quali l’attività solare è stata più intensa e approssimativamente sono:
- 1727-1788;
- 1837-1870;
- 1937-2000.
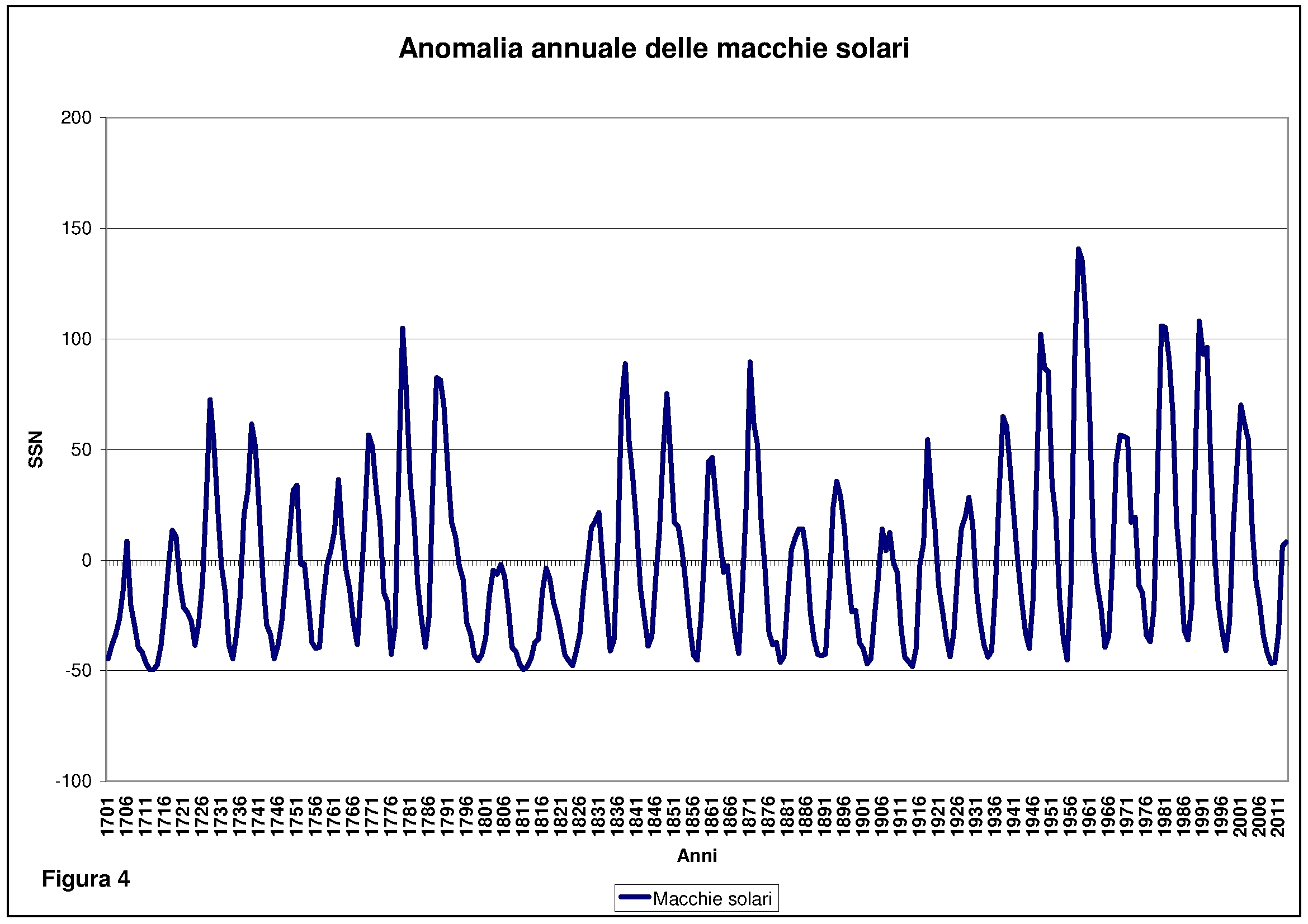
L’ultimo appare essere anche quello in cui l’attività è stata più intensa. Calcolando la media delle macchie per l’intero periodo si è proceduto ad ottenere la relativa anomalia. Il numero medio annuo di macchie si attesta a 49,54 quindi lo fissiamo come punto di riferimento arbitrario per stabilire un’attività solare alta o bassa come da figura 4.
Ora possiamo affinare quanto precedentemente osservato, per cui i tre periodi di attività solare più elevata appaiono essere:
- 1726-1792;
- 1835-1873;
- 1936-2004.
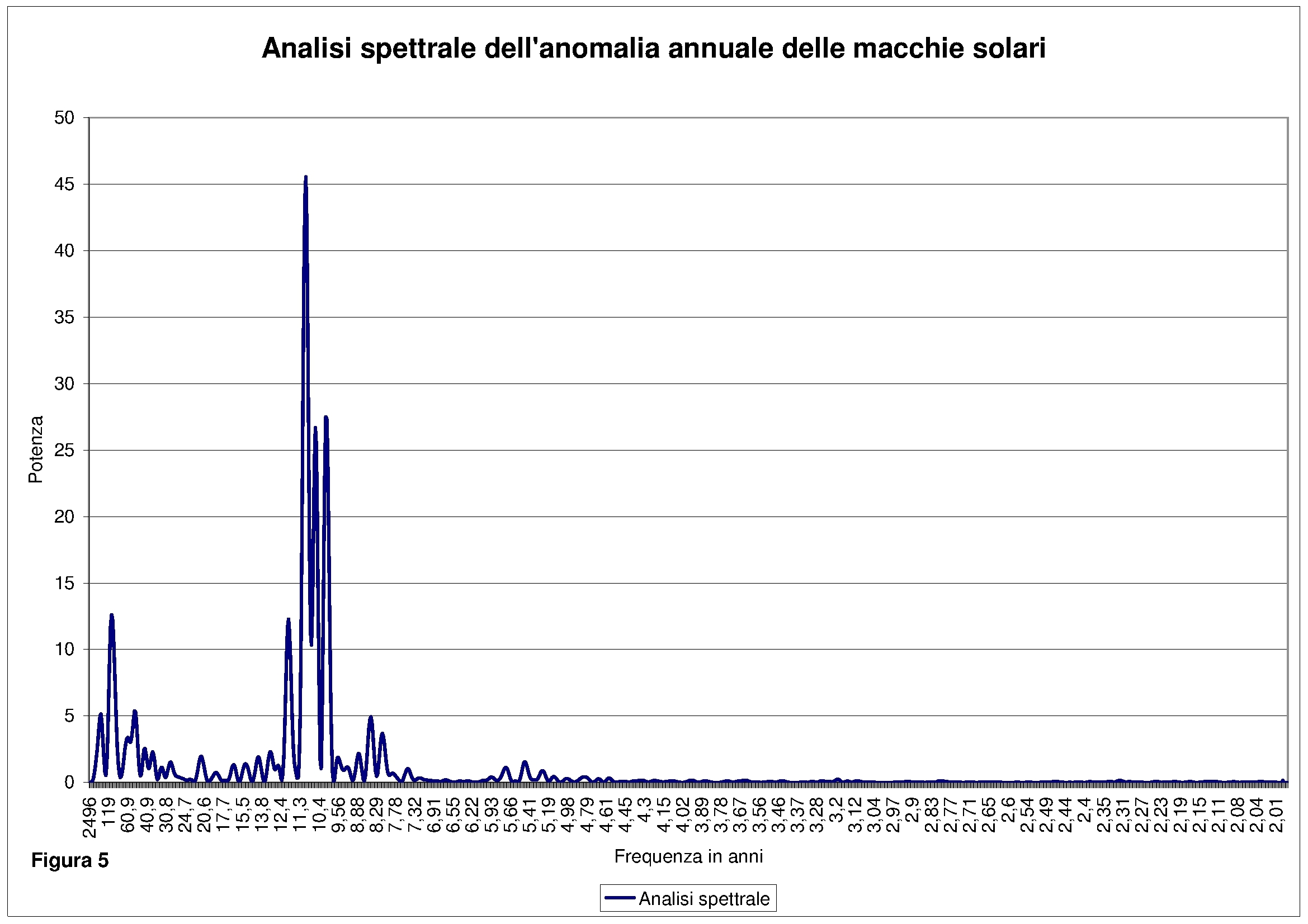
A questo punto cerchiamo di analizzare lo spettro di potenza della variabile SSN come visibile in figura 5. Come nelle attese si riscontra un picco di potenza ad 11 anni ed anche tra i 10 e i 12 anni. Il nostro interesse è però rivolto ai segnali di bassa frequenza e comunque superiori ai 22 anni.
In figura 6 è possibile visualizzare lo spettro fissato sui segnali con frequenza superiore ai 25 anni. Da questo zoom grafico si notano chiaramente alcune frequenze che in parte divideremo, come per le anomalie di temperatura, in gruppi.
Di seguito le fasce di frequenza:
- compresa tra 356,56 e 146,82 con picco a 192 anni;
- compreso tra 131,36 e 80,51 con picco a 104 anni;
- 60,87 anni;
- 52 anni;
- 42,30 anni;
- 37,25 anni;
- 32,84 anni;
- 29,36 anni.
Come noto la variabilità più evidente dell’attività solare è il ciclo di circa 11 anni delle macchie solari. Questa ciclicità mostra però delle variazioni nel tempo così come ben riscontrabile dalle figure 3 e 4. Oscillazioni nel lungo termine possono produrre variazioni tali da influenzare il clima terrestre. L’importanza della conoscenza circa le motivazioni alla base delle variazioni dell’attività solare possono meglio fare luce sulle dinamiche complesse di interazione tra il clima terrestre e il sole. Alla base del meccanismo responsabile della variazione dell’attività solare c’è la conversione da campo magnetico poloidale a campo magnetico toroidale e nuovamente a campo poloidale con polarità invertite. La velocità assunta dalle celle di circolazione superficiale e profonda determina l’ampiezza e il periodo del ciclo delle macchie solari. La velocità di flusso meridionale superficiale verso i poli determina una modifica nell’ampiezza del ciclo delle macchie solari, ma cosa modifica la velocità del flusso e quindi dei cicli solari?
Non si dispone dei dati della velocità del flusso superficiale meridionale del plasma solare ma si ipotizza che l’alternarsi dei vari cicli orbitali dei pianeti esterni possa modificare in maniera significativa la forza planetaria di marea la quale è in grado di modificare i flussi meridionali superficiali e profondi alla base del’attività solare. Il dichiarato intento di questa ricerca sarà quello di individuare almeno alcune delle cause che si evidenziano attraverso le frequenze emerse nell’analisi spettrale di cui sopra.
Rivolgiamo la nostra attenzione ai pianeti esterni Giove, Saturno, Urano e Nettuno. Giove è il più grande dei pianeti di tutto il sistema solare la cui massa è circa 2,5 volte la massa di tutti gli altri pianeti messi insieme. Il baricentro del sistema solare è influenzato da Giove e dai pianeti esterni gassosi. Il baricentro Sole-Giove cade esternamente alla nostra stella ma la sua posizione varia in relazione alla posizione assunta dai vari pianeti nel corso delle loro orbite. Qui di seguito si elencano i periodi siderali dei vari pianeti esterni:
- GIOVE 11,862615 anni
- SATURNO 29,447498 anni
- URANO 84,016846 anni
- NETTUNO 164,79132 anni
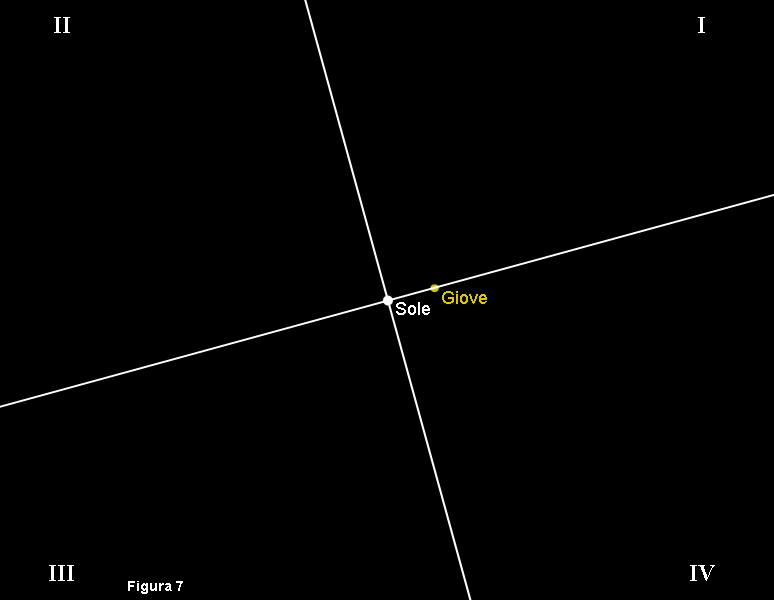
Nella rappresentazione eliocentrica con una visione ortogonale del piano orbitale si decide di suddividerlo in quattro quadranti per comodità nella registrazione e interpretazione delle posizioni planetarie. Per la costruzione degli assi si decide di utilizzare i punti di perielio e afelio di Giove ove passa l’asse orizzontale. Ortogonalmente a tale asse, e passante per il sole, si traccia la retta dell’asse verticale, il tutto visibile in figura 7.
Conoscendo i periodi siderali dei vari pianeti possiamo calcolare gli allineamenti secondo la formula:
Pa= (Pe*Pi)/(Pe-Pi)
dove Pa= periodo di allineamento, Pe=periodo siderale pianeta esterno, Pi=periodo siderale pianeta interno.
Dall’applicazione della formula si ricavano i seguenti periodi di allineamenti planetari:
- Giove-Saturno 19,865 anni
- Giove-Urano 13,813 anni
- Giove-Nettuno 12,783 anni
- Saturno-Urano 45,338 anni
- Saturno-Nettuno 35,855 anni
- Urano-Nettuno 171,406 anni
Questi periodi possiamo definirli come “battiti di frequenza fondamentali”.
Vista la particolare importanza di Giove e del pianeta esterno a lui più vicino, Saturno, analizzeremo con maggiore dettaglio i legami tra questi due pianeti nel periodo di rivoluzione attorno al Sole alla ricerca di ulteriori particolari periodi che chiameremo “nodi di frequenza”.
Giove e Saturno compiono un allineamento ogni 19,865 anni. Essendo le loro orbite non perfettamente circolari compiono la loro rivoluzione con tempi leggermente diversi in funzione al loro avvicinamento o allontanamento dai rispettivi punti di afelio o perielio e questo determina una leggera differenza nel tempo dei loro allineamenti che comunque si realizzano nel tempo medio sopra descritto di 19,865 anni. Ogni allineamento non avviene nelle stessa posizione celeste e per quanto ci riguarda nello stesso quadrante, come da suddivisione in figura 7, ma avviene anticipando di un angolo di circa 117,0033° spostando l’allineamento successivo in un diverso quadrante. Questo spostamento determina una particolare sequenza di allineamenti nei vari quadranti. Detto ciò si può calcolare che un allineamento avvenuto in un dato quadrante si ripresenta sullo stesso in media ogni 59,58 anni, ovvero 3 allineamenti di Giove-Saturno, ma visto che ogni sequenza di allineamenti si compie su 351,0099° si introduce una inevitabile irregolarità nelle sequenze pari a 8,99° tra una triade e la successiva. Questo determina un periodo di sequenza completo degli allineamenti Giove-Saturno con ritorno nello stesso quadrante, nello stesso punto celeste e con inizio di un nuovo ciclo sequenziale dopo 2383,45 anni ovvero dopo 120 allineamenti Giove-Saturno o 40 allineamenti nelle sequenze di 59,58 anni.
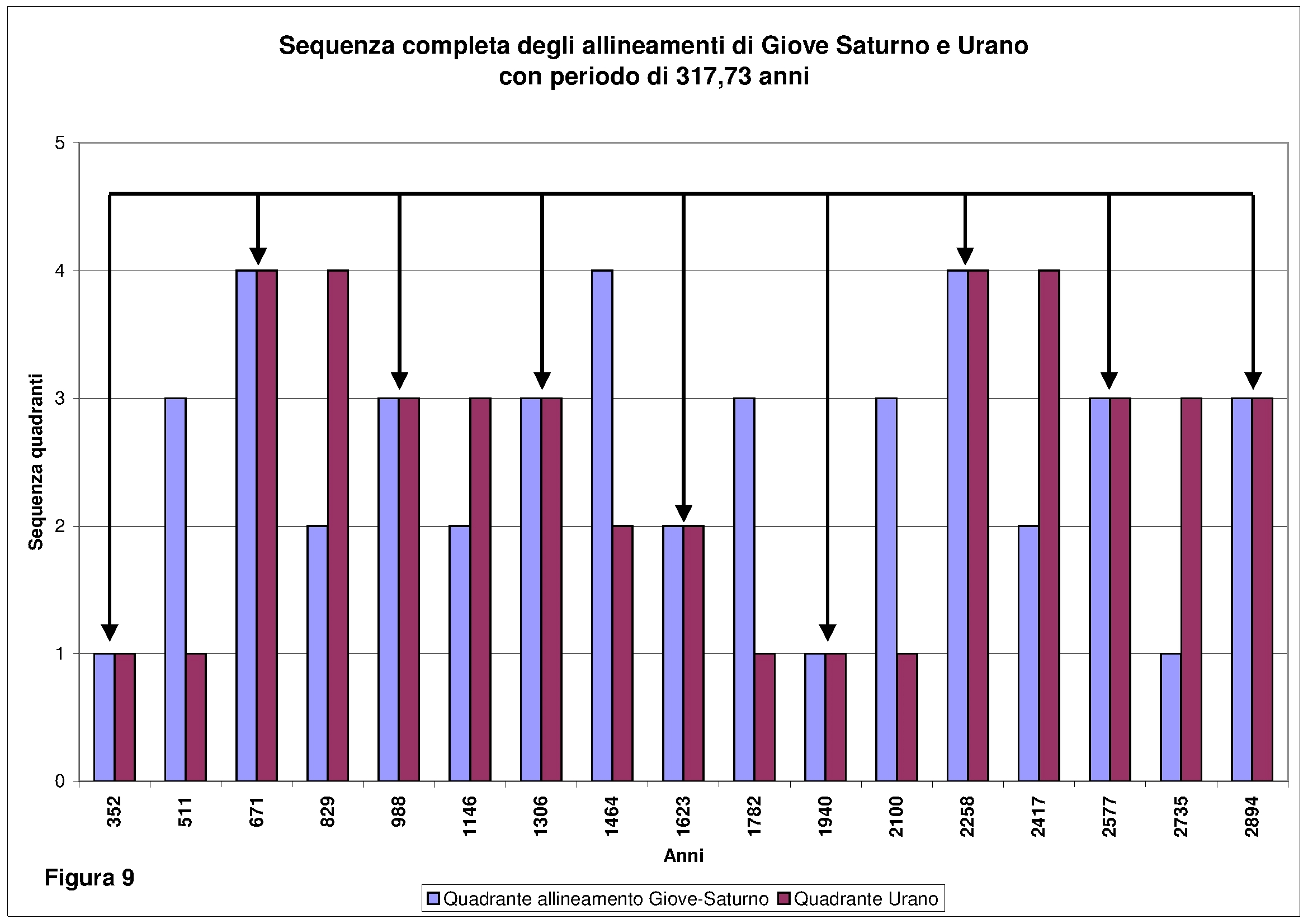
Un ulteriore nodo di frequenza è dato dalla sequenza di allineamenti ottenuti sulla base di tre allineamenti di 59,58 anni e pari a 178,74 anni. In verità questa frequenza è anche la stessa affinché Urano si presenti nello stesso quadrante di allineamento di Giove e Saturno. L’intera sequenza del passaggio dei relativi allineamenti nei quattro quadranti è visibile in figura 8. La caratteristica di questa sequenza è data dal passaggio ripetuto per 3 volte sullo stesso quadrante intervallato da una sequenza anomala di quattro volte. Altro importante nodo di frequenza è dato dall’allineamento di Giove e Saturno con Urano nello stesso quadrante. La frequenza di questi allineamenti è di 317,73 anni, chiaramente visibile in figura 9.
In realtà questa sequenza contiene un nodo a più bassa frequenza di 1587,49 anni che rappresenta il ciclo completo delle sequenze dei tre pianeti nei 4 quadranti. Dalla stessa figura 9 possiamo anche apprezzare la sequenza di allineamenti di Giove e Saturno con frequenza di 158,89 anni. Un’altro nodo di frequenza individuato è la frequenza di 99,33 anni che rappresenta particolari allineamenti di Giove Saturno in determinate sequenze lungo i nostri 4 quadranti. Questa frequenza è importante perché è la base di frequenze più basse collocate a 496,56 – 297,83 e forse la più importante a 794,33 anni che rappresenta la frequenza con cui inizia la particolare sequenza dei quadranti 3-4-2-3-1-2 intervallata da una serie nei quadranti 4-1. La sequenza nei quadranti 3-4-2-3-1-2 presenta una attività solare nel complesso mediamente bassa suddivisa in sensibile attività bassa nei quadranti 2-3 e più alta nei quadranti 1-4 così che quei particolari periodi sono contrassegnati da una maggiore frequenza di allineamenti nei quadranti 2-3 rispetto ai quadranti 1-4. La sequenza è visibile in figura 10.
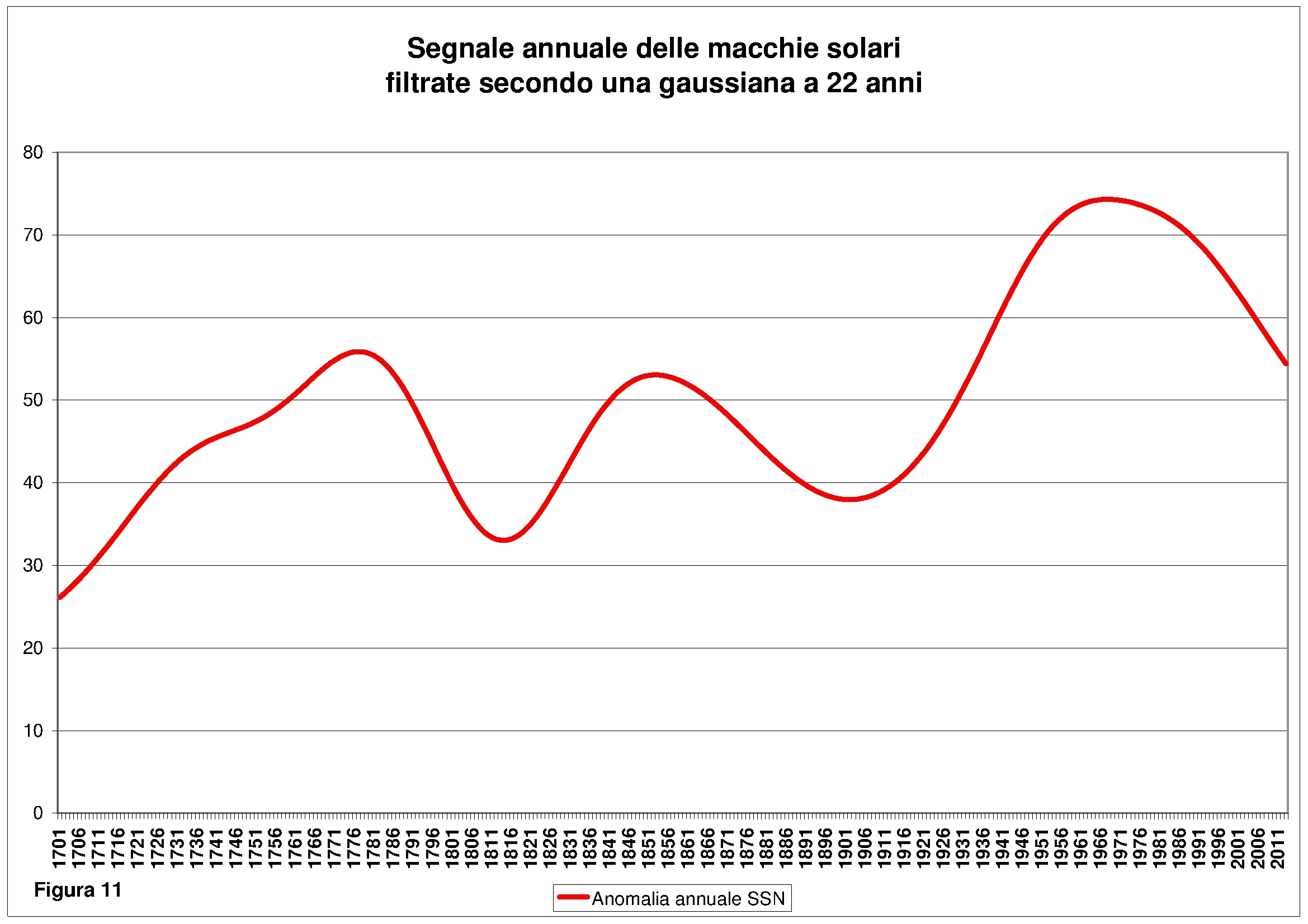
Come detto inizialmente il nostro interesse è nella individuazione di frequenze planetarie a bassa frequenza che verosimilmente possono modulare l’attività solare ad alta frequenza. A questa categoria rientrano a pieno titolo le più note frequenze appartenenti al ciclo di Hale e di Schwabe. Per questa ragione il data-set delle macchie solari è stato sottoposto a filtraggio mediante una gaussiana a 22 anni in modo da evidenziare il segnale portante dell’attività solare a bassa frequenza, vedi figura 11.
Per ogni nodo di frequenza sopra illustrato è stata calcolata la relativa armonica secondo la formula:
y=A*cos(2*∏*(x-x0)/T-p)
dove A=ampiezza, x=anno corrente, x0=anno di riferimento, T=periodo, p=fase.
Le varie armoniche ottenute sono state sommate tra loro. Il risultato rappresenta la sommatoria dei segnali planetari precedentemente individuati. Le due curve, quella del segnale delle macchie solari già visualizzate nel grafico in figura 11 e quella appena individuata “planetaria”, sono state poste in grafico ed il risultato è visibile in figura 12.

Si nota la quasi perfetta corrispondenza. Possiamo ora asserire con sicurezza che le dinamiche planetarie sono responsabili della variabilità dell’attività solare che si esprime attraverso l’alterazione dell’attività magnetica. A questo punto dobbiamo utilizzare le stesse frequenze per descrivere la variazione dell’anomalia della temperatura. In questo caso non tratteremo i dati con nessuna azione di filtraggio ma lasceremo il data-set in versione originale. Seguendo la stessa formula precedentemente usata ovvero:
y=∑A*cos(2*∏*(x-x0)/T-p)
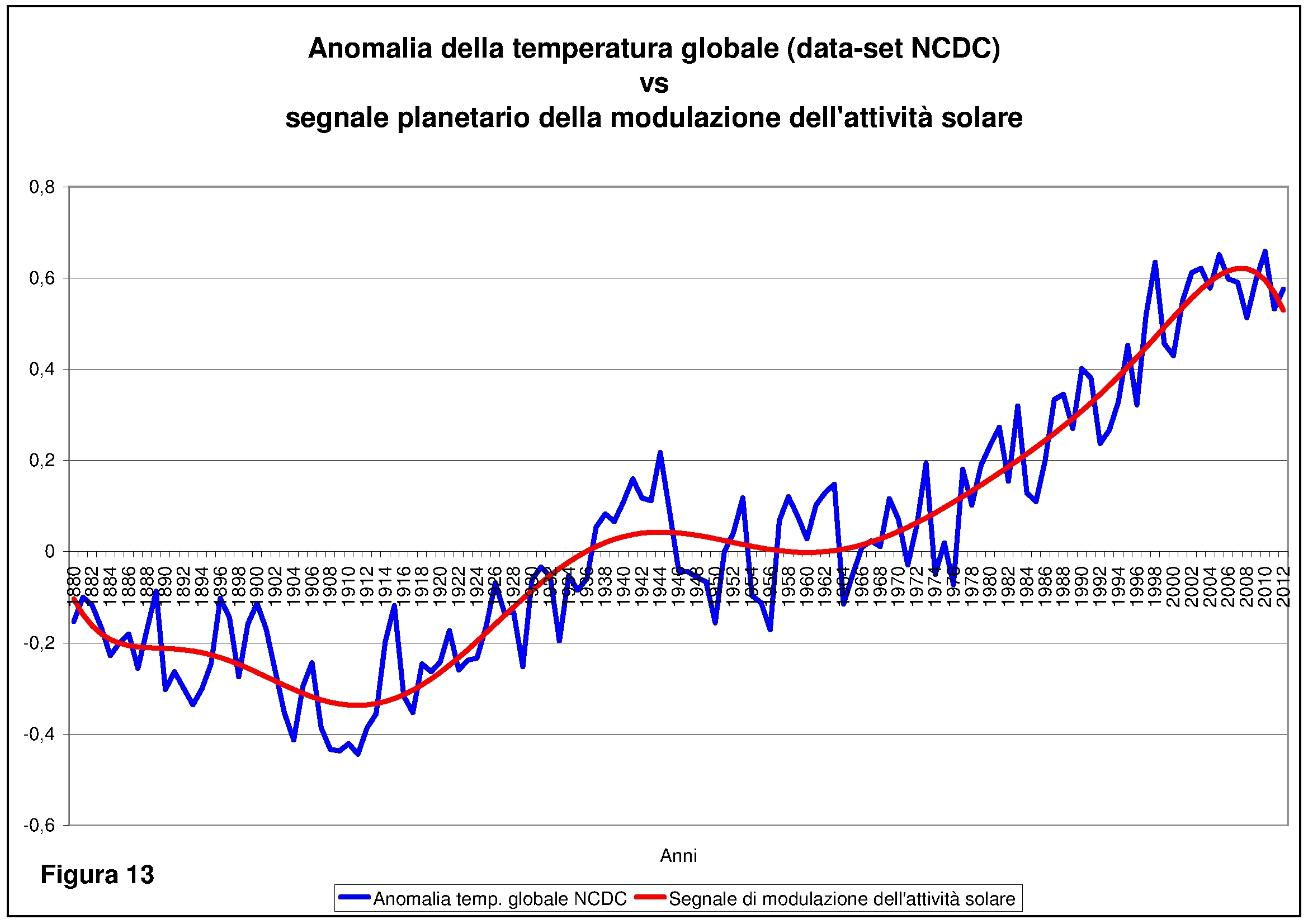
costruiamo il nostro data-set del segnale planetario e lo raffrontiamo a quello originale come visibile in figura 13.
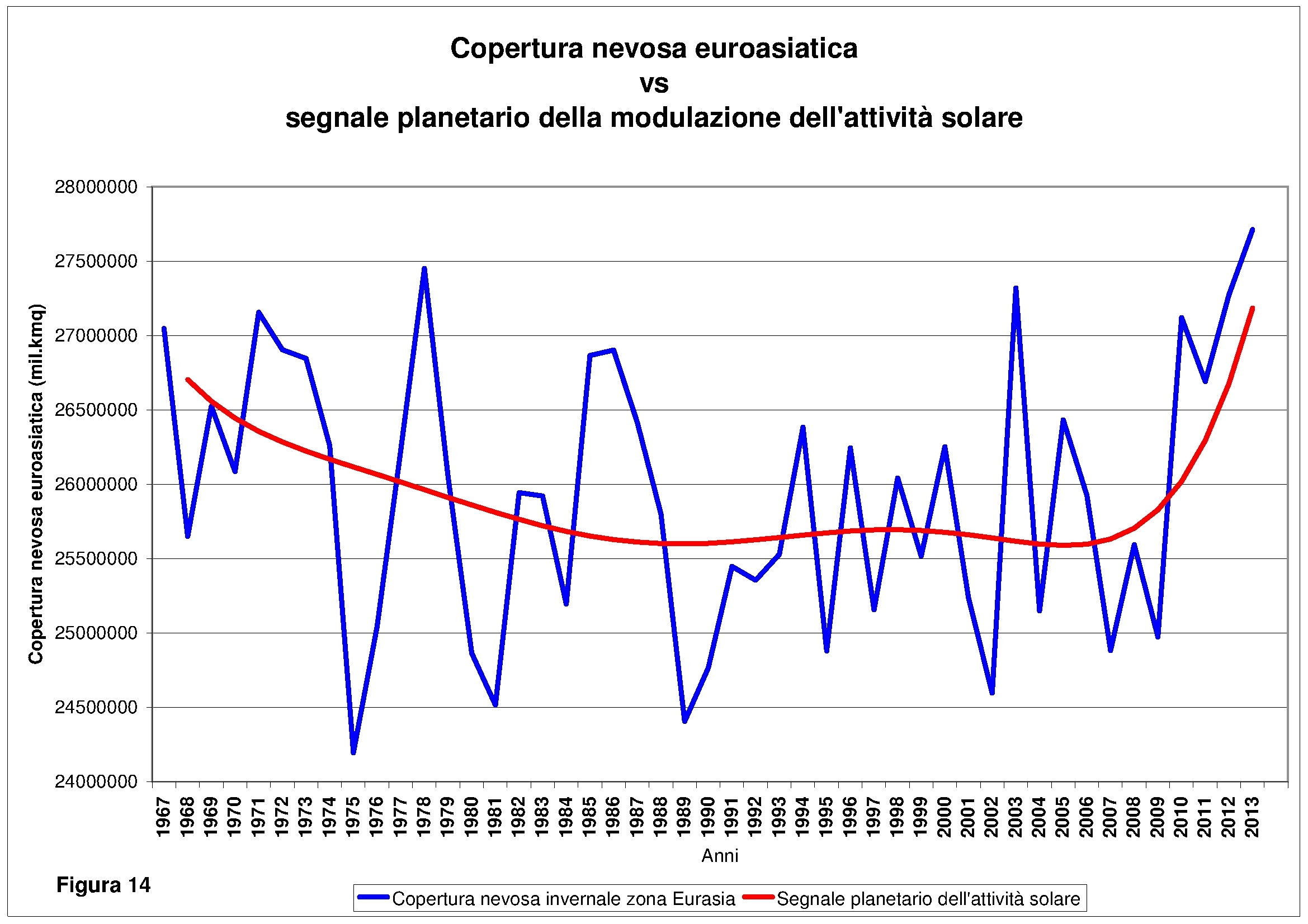
La corrispondenza ottenuta è sorprendente! Visti i risultati si decide di completare la ricerca con il confronto della copertura nevosa nella zona eurasiatica e il segnale planetario di modulazione dell’attività solare. La tecnica usata è la stessa utilizzata per le precedenti variabili. Il risultato grafico è visibile in figura 14. Anche in questo caso la linea del segnale planetario risulta essere tendenzialmente in perfetto accordo con il dato osservato.
Conclusioni
La presente ricerca ha posto a confronto i dati dell’anomalia della temperatura globale secondo il data-set del NCDC con i dati appartenenti al data-set della copertura nevosa sia in zona euroasiatica che nord americana. L’approfondimento dell’analisi dei dati ha mostrato come la variazione della copertura nevosa nella zona euroasiatica sia relazionato con la variazione dell’estensione del vortice polare. Infatti quest’ultimo tende nel tempo ad estendersi o ritrarsi in latitudine in maniera più consistente rispetto alla zona nord americana determinando così una maggiore ampiezza dell’oscillazione della copertura nevosa.
L’attenzione della ricerca si è soffermata nella possibile verifica di una connessione e relazione stretta tra l’attività solare e le variabili di cui sopra. L’individuazione di varie frequenze planetarie ha evidenziato una serie di battiti di frequenza e nodi di frequenza che sono stati utilizzati per la costruzione di un data-set comprendente la sommatoria dei vari segnali e identificato come segnale planetario di modulazione dell’attività solare. Il confronto successivo con tutte le variabili esaminate ha mostrato una sua strettissima correlazione, indice che l’azione planetaria è in grado di influenzare l’attività solare facendo ipotizzare una influenza diretta della forza planetaria di marea in grado di modificare le velocità meridionali superficiali di flusso del plasma solare.
Seguendo la costruzione del data-set della modulazione del segnale planetario per il prossimo futuro si evidenzia come l’interazione planetaria favorevole all’intensa attività solare è conclusa. Lo schema del segnale si avvia ad una fase complessiva, fino alla fine della metà del 2600, in grado di forzare l’attività solare verso una decisa diminuzione. Ovviamente tale linea tendenziale, sempre secondo l’azione planetaria, sarà intervallata da episodi con attività magnetica solare in ripresa ma seguendo una tendenziale in diminuzione. Si attende, quindi, che il segnale della temperatura globale possa seguire tale linea tendenziale.
Nel futuro più prossimo, dal tempo attuale fino al 2100 circa, è attesa un’azione planetaria favorevole ad una bassa attività solare a cui seguirebbe una ripresa fino al 2160 circa. Spingendoci ancora nel futuro e seguendo l’azione planetaria di modulazione del segnale delle SSN si può ipotizzare che il periodo compreso tra il prossimo 2450 e il 2650 (200 anni circa) possa presentarsi del tutto simile a quello conosciuto nella sua estensione massima come Piccola Età Glaciale avvenuto tra il 1650 e il 1850.
Infine possiamo dedurre dai risultati della presente ricerca che lo schema complessivo che induce alla oscillazione e quindi alla variabilità del clima terrestre su base secolare è diretta conseguenza dell’attività solare la quale è modulata dall’azione planetaria. Il sistema climatico terrestre si presenta molto sensibile ai segnali di bassa e bassissima frequenza per la maggiore e profonda incisività delle forzanti che lo costituiscono imponendo un segnale portante ove si modulano tutte le oscillazioni a più alta frequenza.





[…] http://www.climatemonitor.it/?p=31974 […]
It would be nice to see the graph extended back to 1600 and forward to 2100 at least.
Here are the conclusions to my post on April 2 2013 “Global Cooling – Methods and Testable Decadal Predictions ” on my blog at
http://climatesense-norpag.bllgspot.com.
3. Summary
1 Significant temperature drop at about 2016-17
2 Possible unusual cold snap 2021-22
3 Built in cooling trend until at least 2024
4 Temperature Hadsst3 moving average anomaly 2035 – 0.15
5 Temperature Hadsst3 moving average anomaly 2100 – 0.5
6 General Conclusion – by 2100 all the 20th century temperature rise will have been reversed,
7 By 2650 earth could possibly be back to the depths of the little ice age.
8 The effect of increasing CO2 emissions will be minor but beneficial – they may slightly ameliorate the forecast
cooling and help maintain crop yields .
9 Warning !! There are some signs in the Livingston and Penn Solar data that a sudden drop to the Maunder
Minimum Little Ice Age temperatures could be imminent – with a much more rapid and economically disruptive
cooling than that forecast above which may turn out to be a best case scenario.
Note prediction #7 which was arrived at by entirely different methods than in the article above.
Number 7. Impressive.
Tks,
gg
Here sre the summary conclusions of my post on Global Cooling – Methods and Testable Decadal Predictions
on my site
http://climatesense-norpag.blogspot.com/2013/04/global-cooling-methods-and-testable.html
These were reached by a diffrent method but note the prediction of a Maunder minimum at about 2600.
3. Summary
1 Significant temperature drop at about 2016-17
2 Possible unusual cold snap 2021-22
3 Built in cooling trend until at least 2024
4 Temperature Hadsst3 moving average anomaly 2035 – 0.15
5 Temperature Hadsst3 moving average anomaly 2100 – 0.5
6 General Conclusion – by 2100 all the 20th century temperature rise will have been reversed,
7 By 2650 earth could possibly be back to the depths of the little ice age.
8 The effect of increasing CO2 emissions will be minor but beneficial – they may slightly ameliorate the forecast
cooling and help maintain crop yields .
9 Warning !! There are some signs in the Livingston and Penn Solar data that a sudden drop to the Maunder
Minimum Little Ice Age temperatures could be imminent – with a much more rapid and economically disruptive
cooling than that forecast above which may turn out to be a best case scenario.
Una breve nota esplicativa per tutti i commenti fino ad ora giunti.
Per tutti coloro che certamente hanno avuto qualche cenno di insofferenza nel vedere un periodo al posto di una frequenza spiego che la forzatura è stata voluta nell’intento di facilitare la lettura dei dati anche a coloro che non hanno dimestichezza con queste tecniche, ma seguono questo blog, usando nel comune linguaggio termini altrettanto impropri. Per quanto riguarda il segnale planetario per determinare ampiezza e fase mi sono basato sul criterio dei minimi quadrati e decomposizione ai valori singolari.
Caro Carlo, ho letto con moltissimo interesse il suo post e lo trovo davvero interessante e importante. Sono anche io d’accordo con le due critiche precedenti sulla difficoltà di lettura (il chiamare frequenza un periodo ha un po’ complicato la vita anche a me …). Ho provato a seguire il suo ragionamento, almeno fino ad un certo punto, e mi sembra valido. Io trovo numeri un po’ diversi dai suoi (ad esempio l’anticipo di 117.0033° a me viene di 117.1484° e non trovo nello spettro di Lomb delle macchie solari un massimo a 60.87 anni ma a 62.2 anni) ma queste piccole differenze non modificano affatto il suo ragionamento. Purtroppo mi sono fermato davanti al calcolo delle armoniche perché non ho capito come si ricavano l’ampiezza e la fase da mettere nelle formule: a mio parere questoi è un punto critico perché sono loro a definire la pendenza della curva delle temperature (Scafetta introduce un termine quadratico che dà la salita delle temperature, su cui si innestano le armoniche del suo modello e i warmisti dicono che quella forma quadratica non è altro che la crescita della temperatura dovuta alla CO2). Leggendo il suo post mi era sembrato di capire che i due parametri derivassero “naturalmente” dai conti, ma quando ho cercato di riprodurre il tutto non ho saputo come fare. Ho molti dataset su cui tentare di riprodurre il suo modello (gli ultimi sono i dati di pesca nel mare di Bering, per non parlare dei singoli dataset usati da Marcott e soci) e mi piacerebbe capire bene… Comunque complimenti per il suo ragionamento, a mio parere semplice e lineare e per questo importante.
Quando ho letto il suo post venivo dalla lettura di un post qui in cui si dimostra che l’unica cosa che conta è la CO2 e quindi sono particolarmente sensibile ad uno sviluppo che possa dimostrare le cause naturali (e anche antropiche in parte, ovviamente) come principale artefice degli andamenti di temperatura. Franco
Analisi di grande e molto stimolante interesse!
–
Mi permetto un commento meramente “estetico”, con esplicita preghiera di non intenderlo come una critica alla notevole sostanza dell’analisi.
–
Ho un (piccolo) problema con la lettura di alcuni grafici (e tabelle) riportanti le analisi spettrali, dove, sull’asse orizzontale, la “frequenza” viene misurata in “anni” — la dimensione di una frequenza è, per definizione, 1/t — si vuol forse indicare, invece, la lunghezza del periodo?
–
Sopratutto, ma non solo, il secondo grafico, “Spettro di potenza della temperatura globale”, riporta una scala orizzontale la cui non-linearità è di tipo non ovvio ad un primo (e successivo…) esame.
–
Immagino sia una funzione asintotica all’origine del tipo 1/x, ma in tal caso il grafico perde molta interpretabilità — forse varrebbe la pena, se disegnato automaticamente da una serie di dati, di ri-plottarlo usando, per le frequenze, la usuale scala logaritmica.
Pura estetica, ribadisco, ma potrebbe aiutare a godere meglio la robusta sostanza.
Ricapitolando: costruita la curva “planetaria” come sommatoria delle armoniche calcolate con la formula
.
y=A*cos(2*∏*(x-x0)/T-p) (a proposito ∏ sta per prodottoria della frazione successiva?) a)
.
la si è confrontata con la curva rappresentante il segnale annuale delle macchie solari, con quella delle temperature e con quella della copertura nevosa.
.
A questo punto mi sorgono alcuni dubbi:
1) la curva planetaria è la stessa in tutti e tre i casi?
2) se la risposta è affermativa (e tale dovrebbe essere se ho capito bene il ragionamento seguito) perché le tre curve calcolate hanno forma differente?
3) sotto i tre diagrammi leggo: segnale della frequenza planetaria (fig. 12), segnale di modulazione dell’attività solare (figura 13), segnale planetario dell’attività solare (fig. 14). Si tratta di tre funzioni diverse o è sempre la stessa planetaria calcolata come sommatoria delle armoniche calcolate con la formula a)?
.
Un bel post che richiede più di una lettura (il tempo a mia disposizione mi ha consentito di effettuarne solo 1 ed un poco 🙂 ) per essere compreso a fondo, ma che presenta conclusioni piuttosto sorprendenti. Se il segnale dell’attività solare modulata dai pianeti riuscisse effettivamente a replicare in modo così fedele le anomalie di temperatura ci troveremmo di fronte ad un fatto di estremo interesse.
Ciao, Donato.